Rumpf mit Klinkerbeplankung
Zwei Lösungsansätze
von Reinhard Siegel
Juli 2025

Inhalt
Einleitung
1 Klinkerbeplankung – Prinzip
2 Arbeitsboot mit Klinkerbeplankung
2.1 Basisrumpf
2.2 Plankeneinteilung
2.3 Plankenquerschnitte
2.4 Planken
2.5 Rumpffläche in Klinkerform
2.6 Plankenabwicklung
3 Arbeitsboot mit Klinkerbeplankung – erweitert
3.1 Variablen für Dicke und Landung der Planken
3.2 Formeln für Breite der Planken
4 Klinkeraussenhaut-Methode
5 Beispiele
5.1 Beiboot (Plankenquerschnitt-Methode)
5.2 Segelboot (Klinkeraussenhaut-Methode)
Anhang 1 – Flächenmodell nach Sentaufmassen
Anhang 2 – graphische Darstellung der Plankenbreiten
Einleitung
Die Aussenhaut eines Bootes aus Holz kann in verschiedenen Bauweisen gefertigt werden. Es gibt den Leistenbau, den Bau aus formverleimten Funier- oder Sperrholzstreifen, die klassische Karwelbauweise sowie die Klinkerbauweise. Beim Klinkerbau überlappen sich die Planken wie Dachziegel. Die Schiffe der Wikinger wurden nach dieser Methode gebaut. Auch das Folkeboot ist ein bekanntes Beispiel.
Im vorliegenden Tutorium wird zunächst an Hand eines Arbeitsbootes gezeigt, wie man einen Rumpf mit Klinkerbeplankung modellieren kann. Anschließend wird das Verfahren durch die Verwendung von Variablen und Formeln erweitert. Dann wird eine Methode vorgestellt, wie sich eine Rumpfoberfläche konstruieren läßt, die lediglich nach einem Klinkerbau aussieht (GfK-Boot). Zwei weitere Beispiele für Klinkerboote schließen das Tutorium ab.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Klinkerbeplankung – Prinzip
Wenn wir in MultiSurf einen Bootsrumpf modellieren, der in Karwelbauweise gebaut werden soll, müssen wir uns im Allgemeinen nicht um die einzelnen Planken kümmern. Es genügt, die Linien für eine Rumpffläche zu erzeugen, die die gewünschte Form hat. Die Einteilung der Fläche in Planken wäre dann eine Aufgabe beim praktischen Bau des Bootes. Dies kann aber auch, falls für die Arbeitsvorbereitung gewünscht, in MultiSurf erfolgen. Siehe hierzu:75 sqm Yacht – from screen to sea
Wollen wir dagegen einen Bootsrumpf mit Klinkerbeplankung modellieren, müssen wir jede einzelne Planke konstruieren. Entsprechend groß ist der Aufwand. Der Aufbau des Modells entspricht dabei dem Vorgehen in der Praxis. Ausgangspunkt ist eine rundspantige Rumpfgeometrie. Diese Basisfläche wird um die Plankendicke nach innen versetzt (Offset Surface; Versatzfläche). Sie wird von einer Reihe von Spanten geschnitten, den Mallen. Zusammen mit Vor- und Hintersteven sind diese Mallen die Stützkurven der Planken.
Bedingt durch die Überlappung der Planken müssen wir mit der untersten Planke beginnen. Ihre Innenseite verläuft mit der Unterkante in der Sponung von Vorsteven und Kiel, die Oberkante liegt auf der Versatzfläche. Bei allen weiteren Planken verläuft die Unterkante innen auf der Aussenseite der vorherigen Planke, ihre Oberkante innen liegt auf der Versatzfläche.
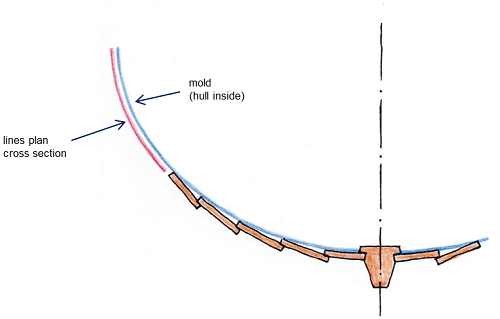
Klinkerbauweise – überlappende Planken
Entsprechend der Anzahl und der Breite der Planken wird das mittlere Mall eingeteilt. Die anderen Mallen erhalten die gleiche relative Teilung. Verbindet man korrespondierende Teilungspunkte, entstehen Kurven in Längsrichtung für die Oberkanten der Planken-Innenseiten. Diese Kurven werden im Folgenden Plankennähte genannt.
Aus allen Richtungen betrachtet sollten diese Kurven harmonisch verlaufen. Ihr Abstand zueinander sollte sich gleichmäßig ändern. Da durch ihre Überlappung die Kanten der Planken sehr deutlich zu sehen sind, bestimmen die Plankennähte darum grundlegend das Erscheinungsbild der Klinkeraussenhaut.
Der Verlauf der Plankennähte sollte regelmäßig sein, was hier nicht der Fall ist..
Am Vorsteven werden die Planken im Bereich der Landung ausgeklinkt, so dass sie ohne Überlappung in die Sponung einlaufen können. Wahlweise wird auch an den Plankenenden am Heck so verfahren.
Einlauf der Klinkerplanken in die Sponung des Vorstevens
Im Folgenden wird am Beispiel eines Arbeitsbootes gezeigt, wie sich ein Rumpf in Klinkerbauweise modellieren läßt. Zunächst wird der Plankenverlauf für den rundspantigen Basisrumpf erzeugt, anschließend werden Innen- und Aussenseiten der Planken definiert.
2 Arbeitsboot mit Klinkerbeplankung
2.1 Basisrumpf
Grundlage für das gewählte Beispiel sind Aufmasse für ein Arbeitsboot aus dem Lehrbuch Bootsbau und Holzschiffbau (J. Börms; Hamburg: Verlag Handwerk und Technik, 1960).
Im Anhang Flächenmodell nach Sentaufmassen dieses Tutoriums werden die einzelnen Arbeitsschritte gezeigt, um an Hand von Aufmassen für Senten die Rumpfoberfläche zu erzeugen. Das Ergebnis ist Modell clinker-0.ms2 mit der C-spline Lofted Surface base_hull.
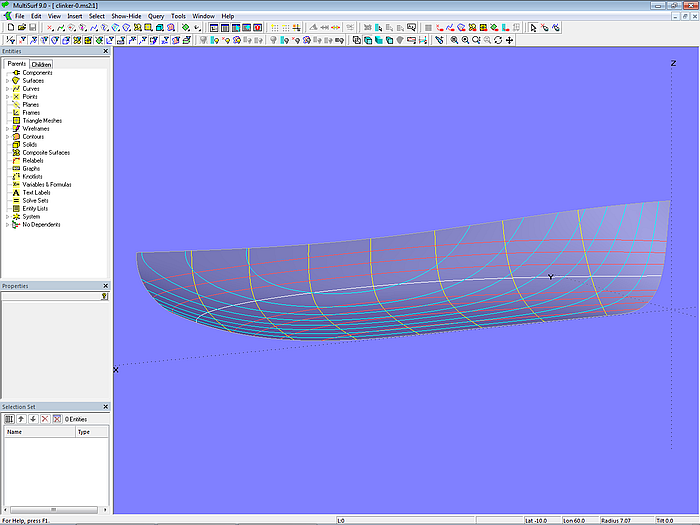
Modell clinker-0.ms2 – Basisrumpf des Arbeitsbootes
Da im Weiteren aus Modell clinker-0.ms2 lediglich die Rumpffläche benötigt wird, werden Spanten, Wasserlinien etc. gelöscht und das Modell unter dem Dateinamen clinker-1.ms2 abgespeichert.
2.2 Plankeneinteilung
Zur Konstruktion des Rumpfes muß die Anzahl der Planken festgelegt werden. Für den Verwendungszweck sowie die Größe des hier gewählten Bootes wird eine Anzahl von 10 Planken je Rumpfseite angenommen. Die Dicke der Planken soll 0,010 m betragen, die Überlappung der Planken das 1,7fache der Dicke (0,017 m).
Mallen
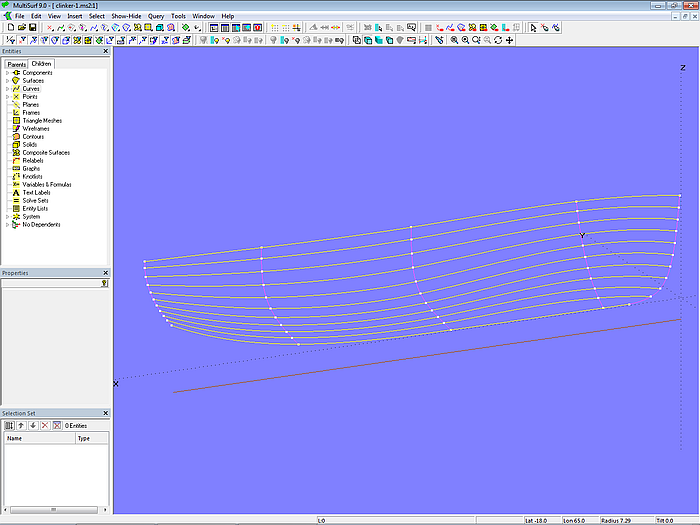
Nun muß der Verlauf der Planken bestimmt werden. Bei einer Anzahl von 10 Planken benötigen wir 9 Plankennähte. Zunächst wird die um die Plankenstärke zum Basisrumpf nach innen versetzte Offset Surface base_hull_off erzeugt. Entlang der Vorderkante von base_hull_off verläuft als Innenkante der Vorstevensponung die EdgeSnake mold_1, entlang der Hinterkante die EdgeSnake mold_5. Zusammen bilden sie die äußeren Mallen. Nun werden auf der Line baseline die drei XYZBeads x_mold_2, x_mold_3 und x_mold_4 gesetzt. Sie bestimmen die Position der inneren Mallen mold_2, mold_3 und mold_4, erzeugt durch Intersection Snakes in Spantebene. Diese Snakes liegen ebenfalls auf der Offset Surface base_hull_off.
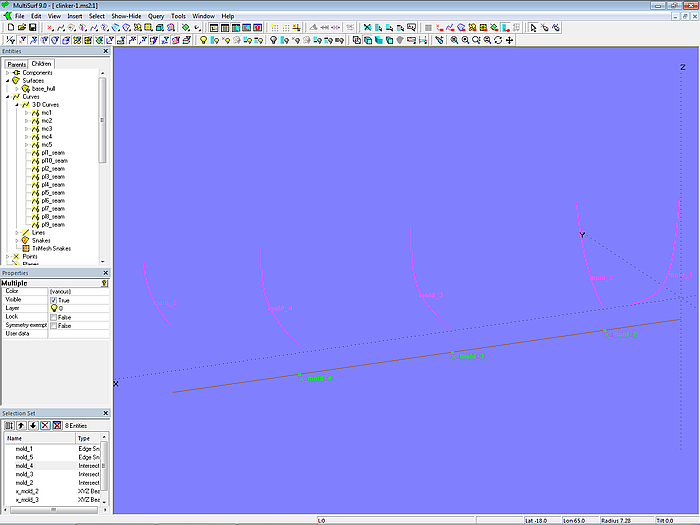
Modell clinker-1.ms2 – Mallen für die Einteilung der Rumpffläche in Planken
Mallpunkte – gleicher Abstand
Nun benötigen wir auf den Mallen Punkte, durch die die Plankennähte verlaufen sollen. Nehmen wir hierfür an, an jedem Mall sollen die Planken gleiche Breite haben. Dann muß die Bogenlänge (Gurtmaß) des Malls in 10 gleiche Teile geteilt werden.
Dazu werden zunächst Rings an den Anfang (t = 0) (m1_r0, m2_r0, ... m5_r0) und das Ende (t = 1) (m1_r10, m2_r10, ... m5_r10) von jedem Mall gesetzt. Wählt man ein zusammengehöriges Paar aus, läßt sich die Bogenlänge über Tools/ Measure/ Distance (oder die entsprechende Schaltfläche in der Werkzeugleiste) anzeigen. Zum Beispiel beträgt sie 1,2918 m für Mall 3 und 1,1937 m für Mall 4.
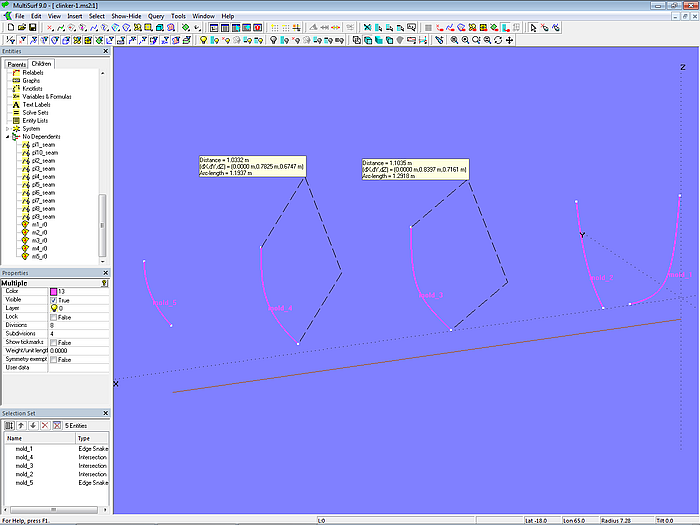
Modell clinker-1.ms2 – Anzeige des Gurtmaßes an den Mallen 3 und 4 über Tools/ Measure/ Distance
Das heißt, wir müssen zum Beispiel auf die Intersection Snake mold_3 9 Punkte setzen. Dazu wird der Punkttyp Arc-length Ring verwendet. Dies sind die Arc-length Rings m3_r1, m3_r2 ... m3_r9. Dabei haben die Punkte m3_r2, m3_r3 ... m3_r9 jeweils den Abstand von 0,1292 m voneinander.
Beim ersten Punkt m3_r1 muß allerdings noch die Landung hinzuaddiert werden; zu m3_r0 beträgt der Abstand dann 0,1462 (0,1292 + 0,0170).
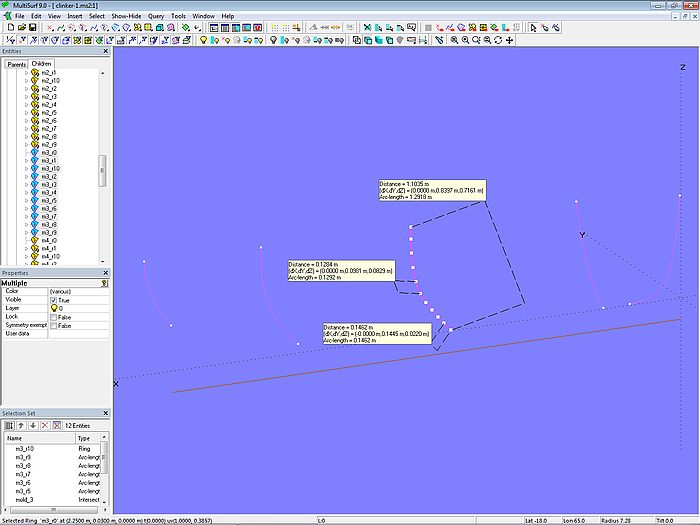
Modell clinker-1.ms2 – Anzeige des Gurtmaßes an Mall 3 und des Abstandes zwischen Mallpunkten
Analog werden die inneren Mallpunkte auf den anderen Mallen erzeugt (m1_r1, m1_r2 ... m1_r9; m2_r1, m2_r2 ... m2_r9; m4_r1, m4_r2 ... m4_r9; m5_r1, m5_r2 ... m5_r9).
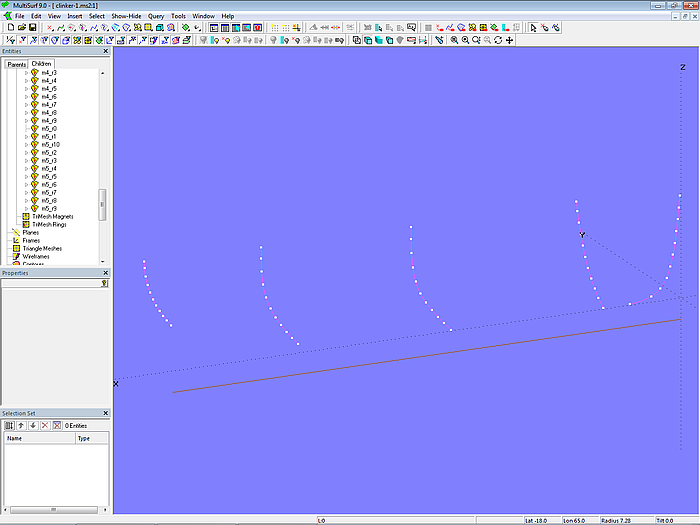
Modell clinker-1.ms2 – Arc-length Rings als Mallpunkte unterteilen das Gurtmaß der Mallen in 10 gleiche Teile.
Plankennähte
Die korrespondierenden Mallpunkte werden dann durch die C-spline Curves pl0_seam bis pl10_seam verbunden.
Das Modell wird nun gespeichert unter dem Dateinamen clinker-1.ms2.
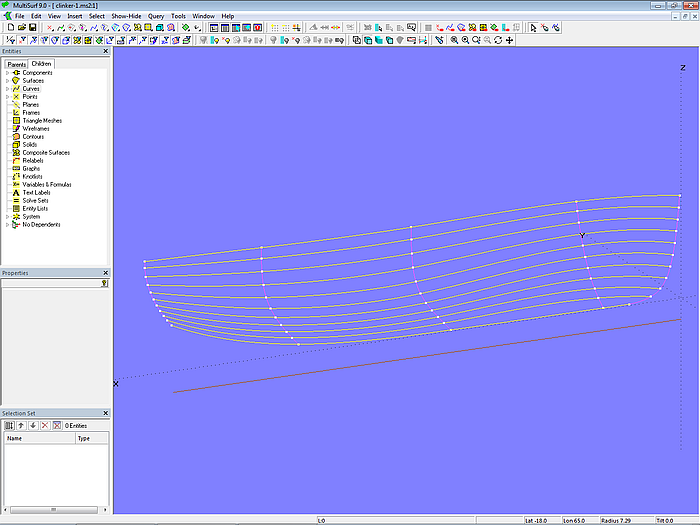
Modell clinker-1.ms2 – die Mallpunkte werden in Längsrichtung mit C-spline Curves zu Plankennähten verbunden.
Die Kurven der Plankennähte haben keine von ihnen abhängigen Objekte. Sie dienen lediglich zur Anzeige, ob sich die Plankenbreiten in Längsrichtung gleichmäßig ändern und der Plankenverlauf gut aussieht. Mit anderen Worten, ob die Mallpunkte an den Mallen harmonisch angeordnet sind. Zum Beispiel verlaufen im Bugbereich die unteren Nähte in der Seitenansicht mit einem Wendepunkt. Durch entsprechende Verschiebung von Mallpunkten kann man versuchen, dies zu korrigieren. Dabei muß aber gleichzeitig darauf geachtet werden, dass sich der Abstand der Mallpunkte entlang einer Mallkurve nicht unregelmäßig verändert.
Graphische Darstellung der Plankenbreiten am Mall
In Modell clinker-1_final.ms2 wird versucht, den S-förmigen Verlauf durch Verschieben von Mallpunkten an Mall 1 und Mall 2 etwas abzumildern. Dies kann nach Augenmaß geschehen, wobei der Nahtverlauf aus unterschiedlichen Richtungen betrachtet wird.
Hierbei kann ein graphische Darstellung hilfreich sein, die anzeigt, wie sich die Plankenbreite über der Malllänge ändert. In Anhang 2 dieses Tutoriums ist die Konstruktion eines derartigen Diagramms beschrieben. Es kann als Komponente diagram_10planks.mc2 über File/ Component/ Load in das Modell eingefügt werden.
In Modell clinker-1_final.ms2 gibt es Diagramme für Mall 1, Mall 2 und Mall 4. Die Positionen der Arc-length Rings für die Mallpunkte lassen sich auch über die Tastatur verändern. Man wählt einen Punkt auf dem Mall aus, so dass seine Eigenschaften im Properties Manager angezeigt werden. Dann klickt man in den rechten Teil der Zeile „Arc dist“; nun kann über Alt-Pfeil auf/ Pfeil ab die Bogenlänge geändert werden. Gleichzeitig ändert sich die Anzeige im Diagramm.
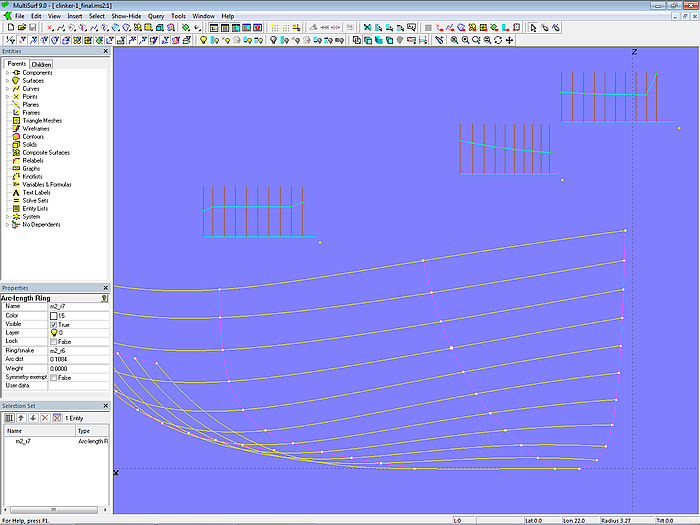
Modell clinker-1_final.ms2 – Strak der Plankennähte mit Hilfe von Diagrammen der Plankenbreite
2.3 Plankenquerschnitte
Speichern wir nun Modell clinker-1_final.ms2 unter dem Dateinamen clinker-2.ms2 ab und fügen im Folgenden die Querschnitte der Planken an den einzelnen Mallen hinzu.
Mall 3
Beginnen wir mit Mall 3 und erzeugen dort die Plankenquerschnitte. Mit entsprechenden Querschnitten an den anderen Mallen dienen sie als Masterkurven für die eigentlichen Planken.
Planke 1 – Querschnitt
Aufgrund der Plankenüberlappung beginnen wir mit der untersten Planke (Planke 1). Ihr Querschnitt liegt mit seiner Innenlinie auf Offset Surface base_hull_off. Aufgespannt zwischen dem 1. Mallpunkt (Arc-length Ring m3_r1) und dem Anfang von Mall 3 (Ring m3_r0) wird sie durch Line pl1_in dargestellt.
Nun wird relativ zu m3_r1 der Offset Point pl1_pt0 erzeugt. Mit m3_r1 (Ende Innenlinie), m3_r0 (Beginn Innenlinie) sowie pl1_pt0 ist nun der 3-point Frame pl1_frame bestimmt. Im Abstand der Plankendicke (0,010 m) zum Ursprung dieses Frames liegt in seiner X-Richtung der Point pl1_pt1. Mit pl1_pt1, m3_r1 und m3_r0 ist nun der Copy Point pl1_pt2 definiert.
Die Aussenlinie von Planke 1 ist Line pl1_out als Verbindunglinie zwischen pl1_pt1 und pl1_pt2. Auf Line pl1_out liegt der Arc-length Bead pl1_e1 im Abstand der Landungsbreite (0,017 m).
Um die Schmiege der Überlappung zwischen Planke 1 und Planke 2 zu erzeugen, wird nun der 2. Mallpunkt (Arc-length Ring m3_r2) mit pl1_e1 durch Line pl2_in verbunden. Diese Line wird von der XY-Ebene von Frame pl1_frame im Intersection Bead pl1_e2 geschnitten.
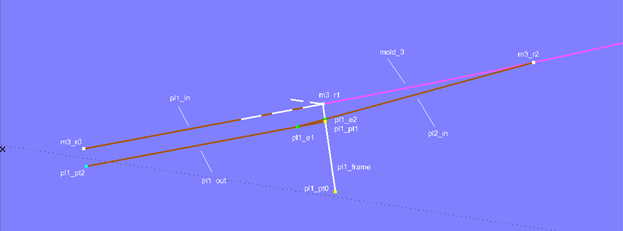
Modell clinker-2.ms2 – Konstruktion der Eckpunkte von Planke 1 an Mall 3
Damit sind alle 5 Eckpunkte von Planke 1 erstellt und sie können durch die B-spline Curve pl1 (Degree = 1) zum Plankenquerschnitt verbunden werden.
Modell clinker-2.ms2 – Querschnitt von Planke 1 an Mall 3
Planke 2 – Querschnitt
Die Konstruktion des Querschnitts für Planke 2 erfolgt in ähnlicher Weise.
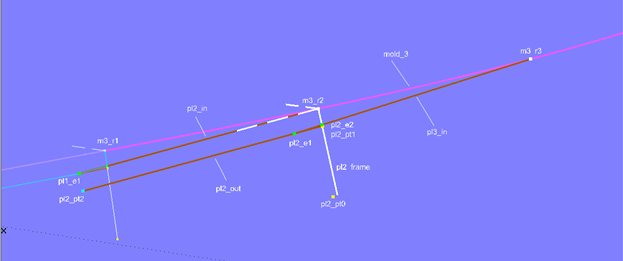
Modell clinker-2.ms2 – Konstruktion der Eckpunkte von Planke 2 an Mall 3
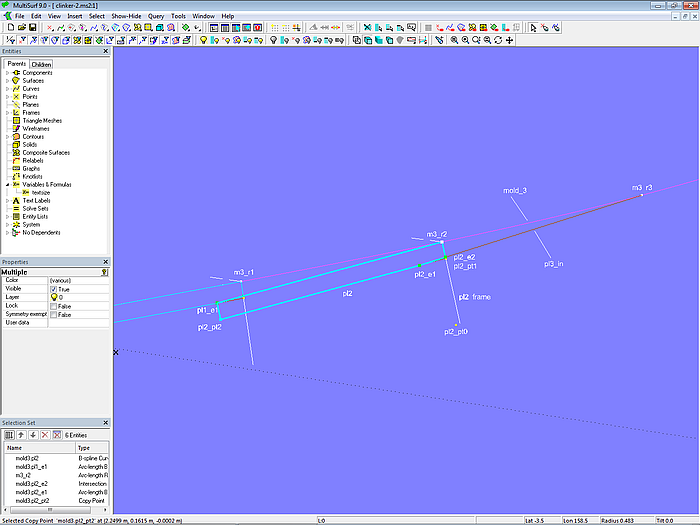
Modell clinker-2.ms2 – Querschnitt von Planke 2 an Mall 3
Planke 3 – Planke 9: Querschnitte
Entsprechend werden die Querschnitte für die Planken 3 bis 9 an Mall 3 konstruiert.
Planke 10 – Querschnitt
Der Querschnitt von Planke 10 ist im Vergleich zu dem der anderen Planken einfach.
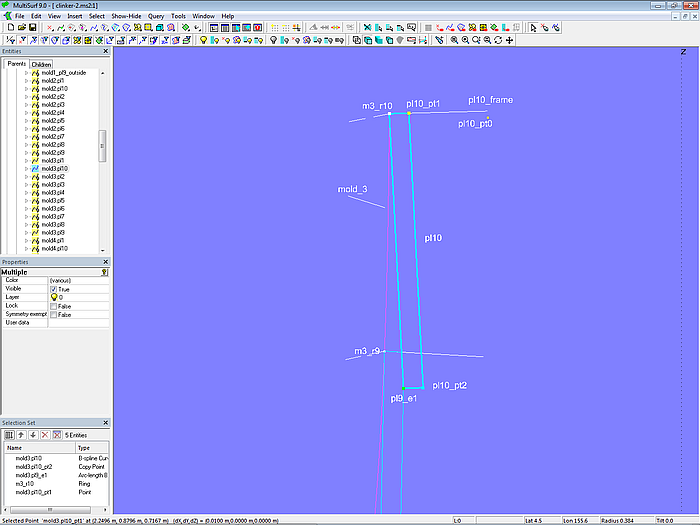
Modell clinker-2.ms2 – Querschnitt von Planke 10 an Mall 3
Damit sind nun alle Plankenquerschnitte von Mall 3 definiert.
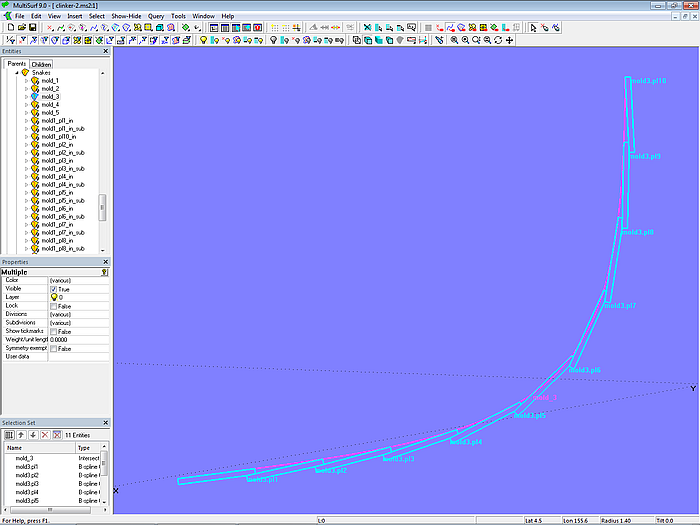
Modell clinker-2.ms2 – Querschnitte der Planken an Mall 3
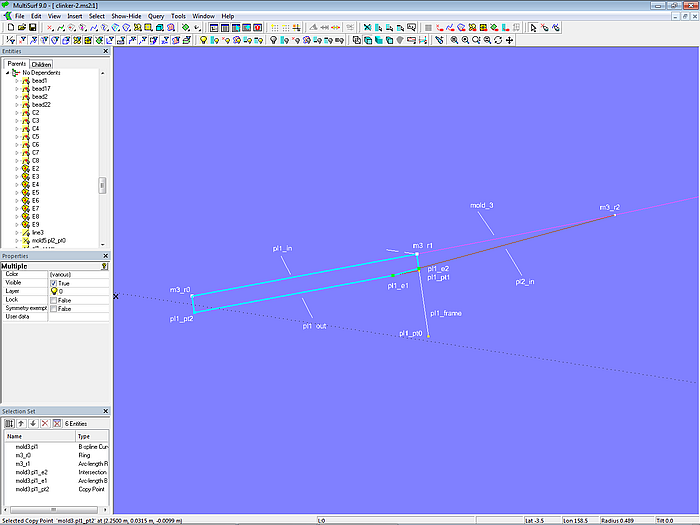
Überprüfen wir nun, wie die Plankeneinteilung mit den zugrundegelegten Annahmen (Mallpunkt-Abstand ist gleich Gurtmaß geteilt durch Plankenanzahl, beim 1. Mallpunkt die Landung hinzuaddieren) von aussen aussieht. Über Tools/ Measure/ Distance lassen wir uns dazu die Abstände zwischen den Mallpunkten und die Abstände zwischen den sichtbaren Plankenkanten anzeigen. Zum Beispiel für Planke 3 zwischen Copy Point mall3.pl2_pt2 und Arc-length Bead mall3.pl2_e1.
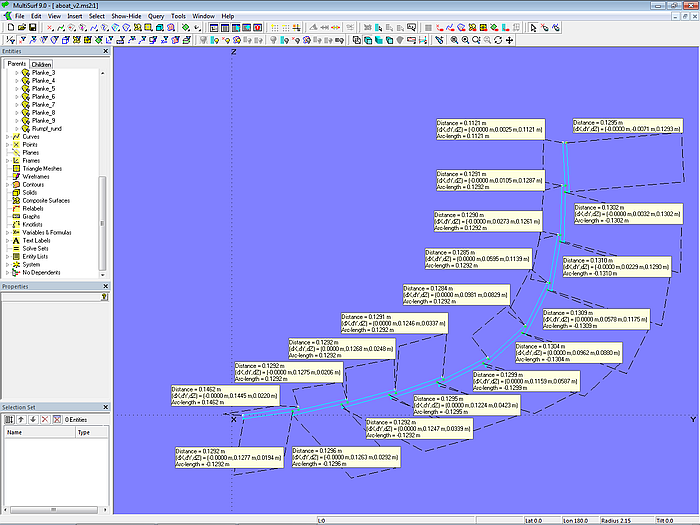
Modell clinker-2.ms2 – Überprüfung der sichtbaren Plankenbreiten
Die Unterschiede zwischen den Plankenkanten in der Breite sind gering.
Mall 2, Mall 4 und Mall 5 (Heck)
Die Plankenquerschnitte an den Mallen 2 und 4 und am Heck (Mall 5) werden auf gleiche Weise konstruiert wie für Mall 3 gezeigt. Da hierfür eine erhebliche Anzahl von Objekten zu generieren ist, ist es praktisch, dies mit Hilfe der Komponente cl_planks-10.mc2 zu bewerkstelligen. Die Eltern dieser Komponente sind der Anfangspunkt der Mallkurve, die folgenden Mallpunkte sowie der Endpunkt der Mallkurve.
Fügen wir zum Beispiel die Plankenquerschnitte für Mall 2 ein. Dazu wählen wir vorab den Mallpunkt am Anfang (Ring m2_r0), die inneren Mallpunkte (Arc-length Rings m2_r1 – m2_r9) und den Mallpunkt am Ende (Ring m2_r10) aus. Dann über File/ Component/ Load die Komponente cl_planks-10.mc2 auswählen, den Dialog Resolving Parents mit OK bestätigen und ohne weiteres Zutun sind die Plankenquerschnitte für Mall 2 generiert.
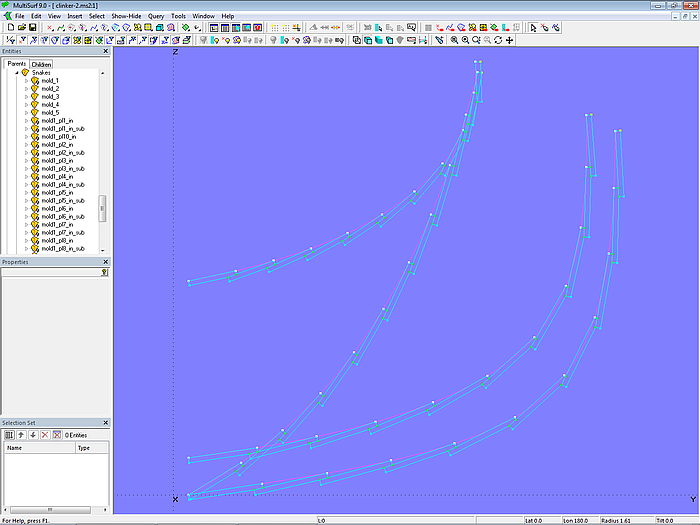
Modell clinker-2.ms2 – Plankenquerschnitte an den Mallen 2 bis 5
Mall 1 (Bug)
Nun benötigen wird nur noch den Anfang der Planken, ihre Front. Am Bugmall sollen sich die Planken aber nicht überlappen, sondern wie beim Karwelbau glatt in die Sponung des Vorstevens einlaufen (siehe Abbildung Kapitel 1). Dazu muß der Landungsteil der Vorderseite mit der Plankenrückseite zusammenfallen, so dass eine Stufe entsteht.
Planke 1 - Front
Beginnen wir mit der Front von Planke 1. Sie ist Teil der Vorstevensponung. Mold_1 ist die Vorderkante (EdgeSnake) der Offset Surface base_hull_off, die um die Plankenstärke nach innen versetzte Fläche des Basisrumpfes base_hull. Diese Kurve ist gleichzeitig die Innenkante der Vorstevensponung.
Analog zu den bereits beschriebenen Mallen liegen auf mold_1 die Rings m1_r0 (Anfang, t = 0) und m1_r10 (Ende, t = 1) und die inneren Mallpunkte m1_r1, m1_r2 ... m1_r9 (Arc-length Rings).
Für die Innenkante der Plankenfront wird mit Ring m1_r0 und Arc-length Ring m1_r1 die SubSnake mold1_pl1_in aufgespannt. Der Abschnitt der Überlappung zwischen m1_r1 und dem Arc-length Ring mold1_pl1_ring ist mit der SubSnake mold1_pl1_in_sub definiert. Der entsprechende Punkt zu mall1_pl1_ring auf der Aussenkante der Sponung (Offset Curve mold1_off) ist der Copy Point mold1_pl1_e1 (gleicher t-Parameterwert). Als Oberkante von Planke 1 beziehungsweise Unterkante von Planke 2 ist zwischen mold1_pl1_ring und mold1_pl1_e1 die Line mold1_pl2_bot aufgespannt. Schließlich ist die Aussenkante der Front die SubCurve mold1_pl1_out (mit den Control Beads mold1_pl1_e0 und mold1_pl1_e1).
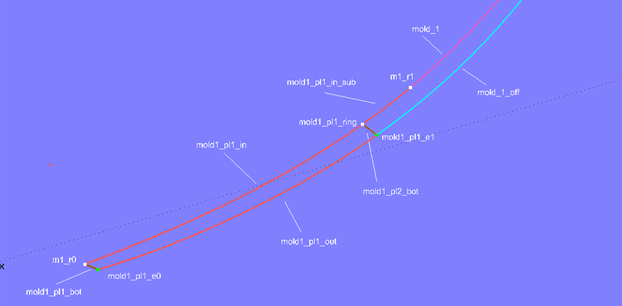
Modell clinker-2.ms2 – Randkurven der Vorderseite von Planke 1
Damit sind alle Kanten der Vorderseite von Planke 1 bestimmt. Mit der PolyCurve mold1_pl1 werden sie zu einem Kurvenzug zusammengefaßt.
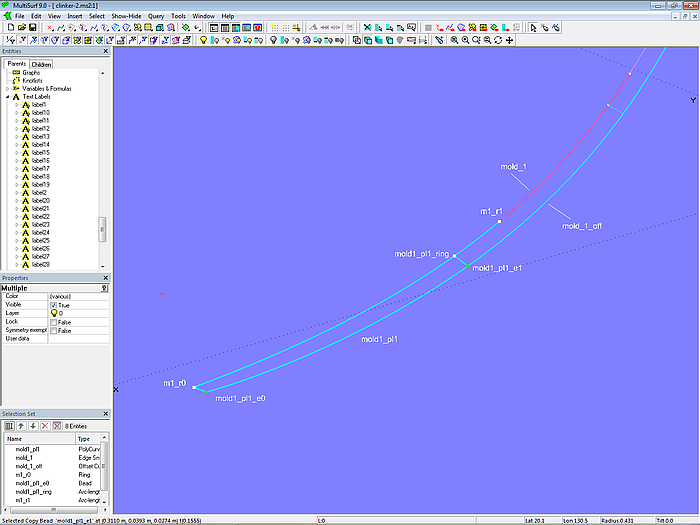
Modell clinker-2.ms2 – zu einem Kurvenzug zusammengefaßte Ränder der Vorderseite von Planke 1
Die PolyCurves für die Front der übrigen Planken 2 bis 9 sind entsprechend konstruiert. Die PolyCurve für die Vorderseite von Planke 10 besteht nur aus 4 Teilkurven.
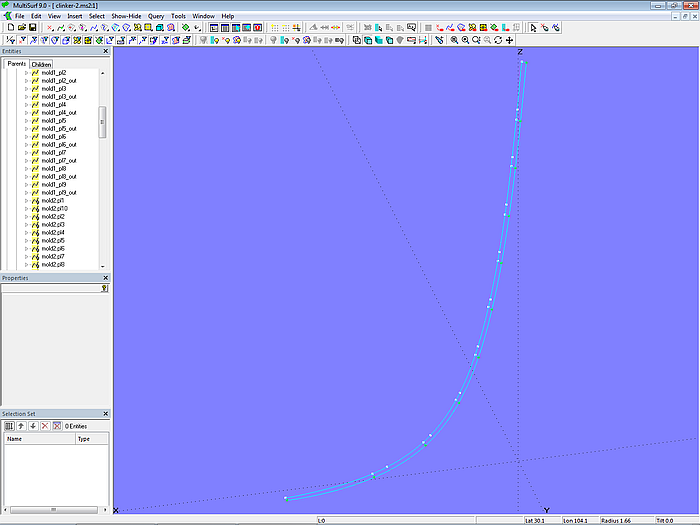
Modell clinker-2.ms2 – Plankenfronten an Mall 1
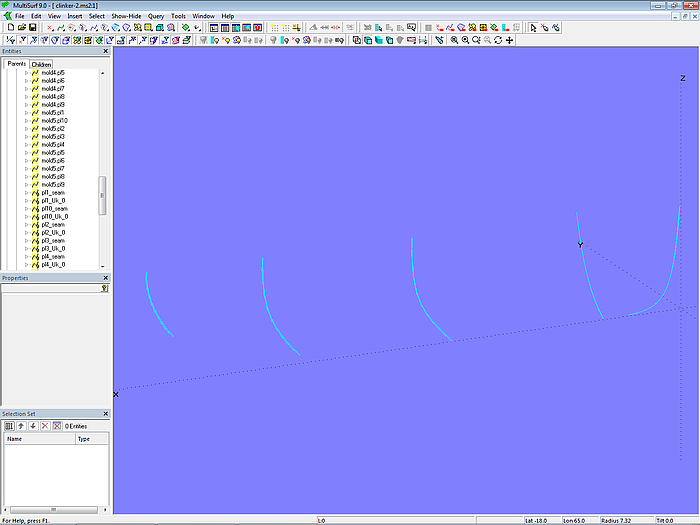
Modell clinker-2.ms2 – Masterkurven der Klinkerplanken
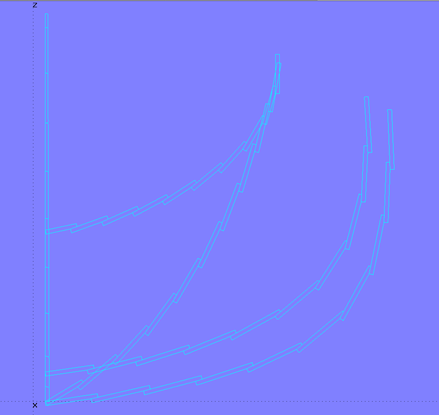
Modell clinker-2.ms2 – Masterkurven der Klinkerplanken
2.4 Planken
Mit diesen Plankenquerschnitten als Masterkurven können nun die einzelnen Planken als C-spline Lofted Surfaces erzeugt werden.
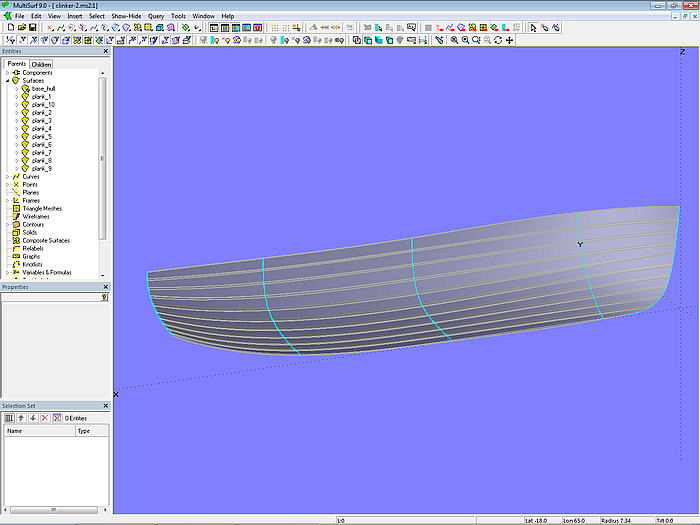
Modell clinker-2.ms2 – Klinkerplanken als C-spline Lofted Surfaces
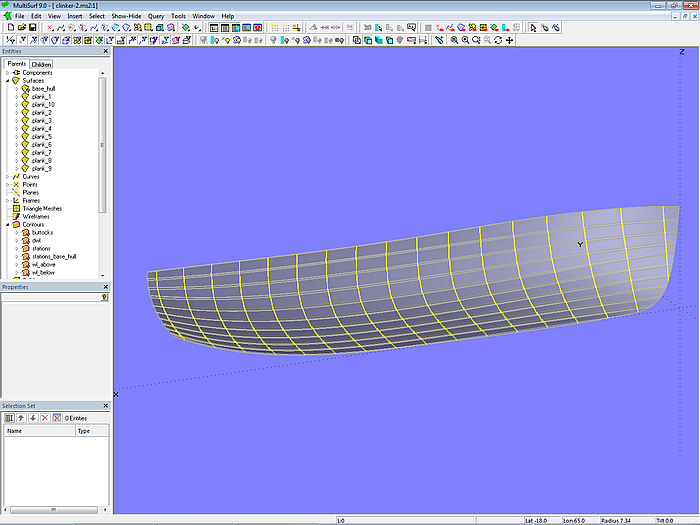
Modell clinker-2.ms2 – Klinkerrumpf
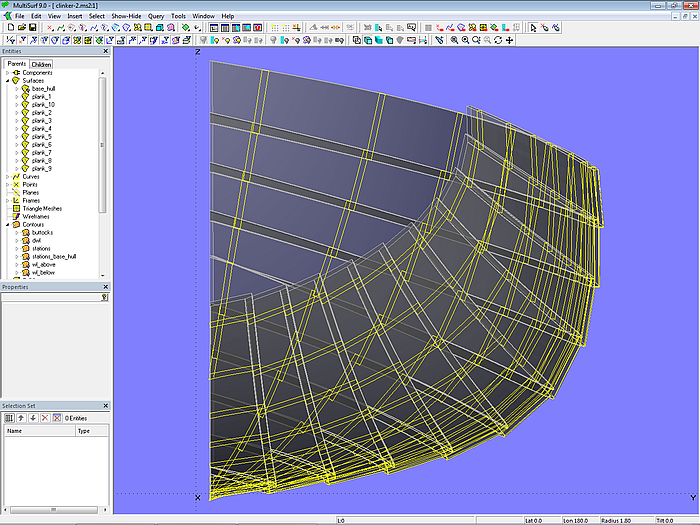
Modell clinker-2.ms2 – Rumpf in Klinkerbauweise
Dies ist Modell clinker-2.ms2.
2.5 Rumpffläche in Klinkerform
Mit einer Auswahl der für die Plankenquerschnitte bereits bestimmten Punkte können Masterkurven für eine C-spline Lofted Surface erzeugt werden, die die komplette Aussenseite des Klinkerrumpfes in einer einzigen Fläche beschreibt. Auf analoge Weise kann die Innenfläche bestimmt werden. Dies ist in Modell clinker-3.ms2 gezeigt.
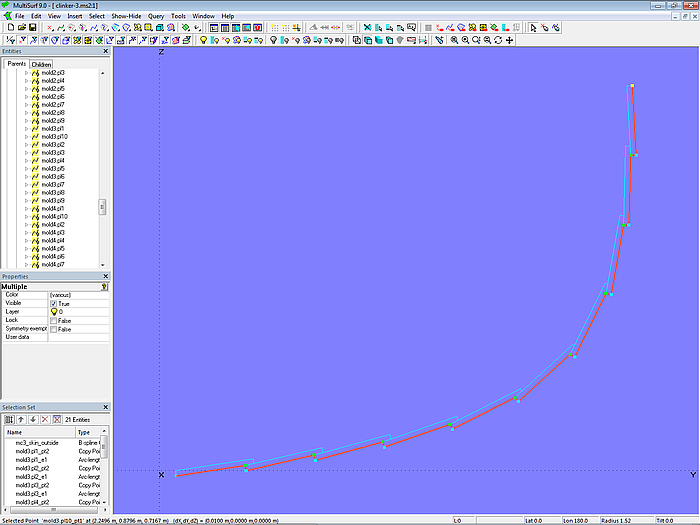
Modell clinker-3.ms2 – Masterkurve an Mall 3 für die Aussenseite des Rumpfes in Klinkerform
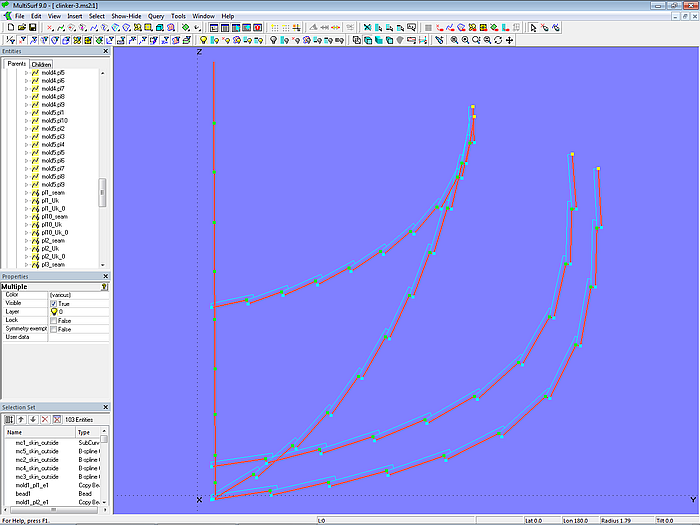
Modell clinker-3.ms2 – Masterkurven für die Aussenseite des Rumpfes in Klinkerform
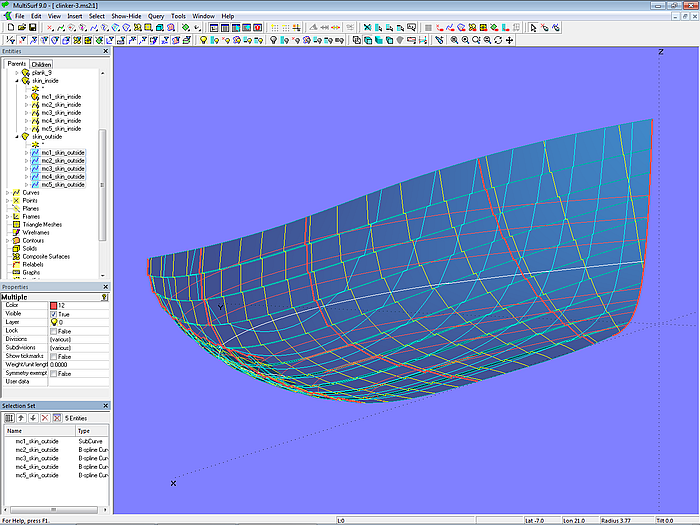
Modell clinker-3.ms2 – Rumpfseite aussen in Klinkerform
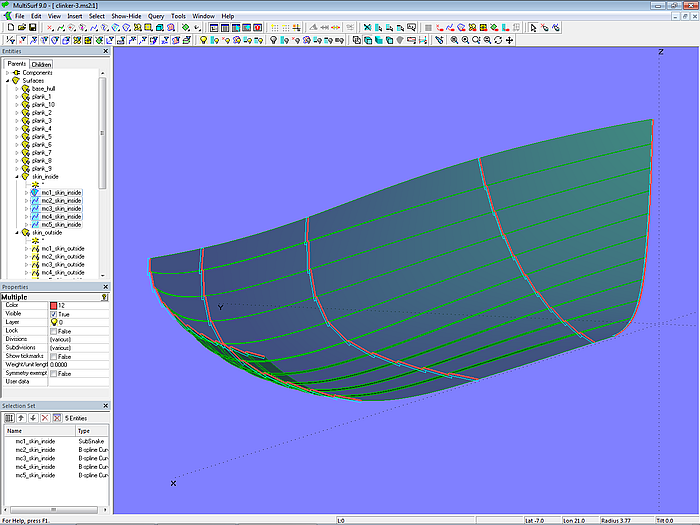
Modell clinker-3.ms2 – Rumpfseite innen in Klinkerform
2.6 Plankenabwicklung
Modell clinker-4.ms2 zeigt, wie sich die Planken verebnen lassen. Zur Abwicklung einer Planke wird zwischen der in Längsrichtung verlaufenden Oberkante und Unterkante der Innenseite eine Developable Surface aufgespannt. Betrachten wir zum Beispiel Planke 3. Oberkante Innenseite ist die C-spline Curve pl3_seam, die im Abschnitt 2.6, Plankeneinteilung, bereits definiert wurde. Unterkante Innenseite ist die PolyCurve pl3_bot_edge, die sich aus der SubSnake mold1_pl3_in (an der Sponung) und der C-spline Curve pl3_bot_edge_0 zusammensetzt. Mit pl3_seam und PolyCurve pl3_bot_edge ist die Developable Surface plank3_dev bestimmt.
Würde man plank3_dev direkt zwischen pl3_seam und pl3_bot_edge_0 aufspannen, wäre die Vorderkante in der Verebnung gerade, und nicht entsprechend der Vorstevenform gekrümmt.
Auf gleiche Weise sind die übrigen Plankeninnenseiten als Developable Surface definiert. Mit dem Flächentyp Expanded Surface können sie anschließend abgewickelt werden.
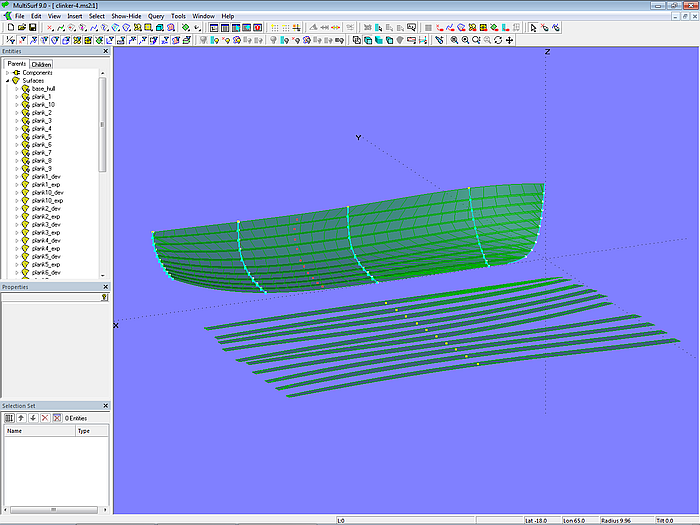
Modell clinker-4.ms2 – Plankenabwicklung
3 Arbeitsboot mit Klinkerbeplankung – erweitert
Im Folgenden wird beschrieben, wie sich mit Variables (Variablen) und Formulas (Formeln) das in Kapitel 2 beschriebene Arbeitsboot-Modell flexibler gestalten läßt.
3.1 Variablen für Dicke und Landung der Planken
In Kapitel 2 werden einfache Annahmen gemacht: alle Planken des Arbeitsbootes haben die gleiche Stärke (0,010 m), die Landung beträgt das 1,7fache der Dicke (0,017 m). Bei der gezeigten Konstruktion der Plankenquerschnitte müssen die Werte für die Plankendicke und die Breite der Überlappung häufig angegeben werden. Verwendet man hierfür Variablen (Variables) und Formeln (Formulas)), lassen sich die Werte einfach ändern und werden überall im Modell entsprechend aktualisiert.
In Modell clinker-5a.ms2 bestimmt die Variable thickness_planks die Stärke der Planken. Variable landing_factor ist der Faktor für die Landung. Die Breite der Landung der Plankengänge berechnet die Formel landing_planks.
3.2 Formeln für Breite der Planken
Bis auf Mall 1 (Vorsteven) wurde bisher für die Plankenbreite die Bogenlänge des jeweiligen Malls über Tools/ Measure/ Distance ermittelt, diese durch die Plankenanzahl geteilt, um dann mit diesem Wert eine Serie von Arc-length Rings als Mallpunkte auf die Mallkurve zu setzen.
In Modell clinker-5a.ms2 ist das Messen durch eine Formel ersetzt. Betrachten wir als Beispiel Mall 3. Ring m3_r0 liegt am Anfang der Kurve, Ring m3_r10 am Ende. Die Formel skin_girth_mold3 mit dem Rechenausdruck: ARCLEN (skin_girth_mold3 / 10, TPOS(m3_r0), TPOS(m3_r10)) berechnet die Bogenlänge (Schmiegeumfang) zwischen beiden Punkten. Entsprechend ermitteln die Formeln skin_girth_mold2, skin_girth_mold4 und skin_girth_mold5 dieses Maß für Mall 2, Mall 4 und Mall 5.
Gleiche Breiten – außer Planke 1
Um die Plankenbreite am Mall zu erhalten, ist die Malllänge durch die Plankenanzahl zu teilen. Mit einer weiteren Formel kann diese Breite ermittelt werden. Beispielsweise definiert die Formel breadth_planks_mold3 diesen Wert mit dem Rechenausdruck (skin_girth_mold3 / 10). Für die Mallpunkte wird dann dieser Formelwert verwendet.
Sollen in der Aussenansicht am Mall alle Planken gleich breit erscheinen, muß für den ersten Mallpunkt noch die Landung zur Plankenbreite addiert werden. Dies erfolgt mit den Formeln breadth_plank1_mold2 ... breadth_plank1_mold5.
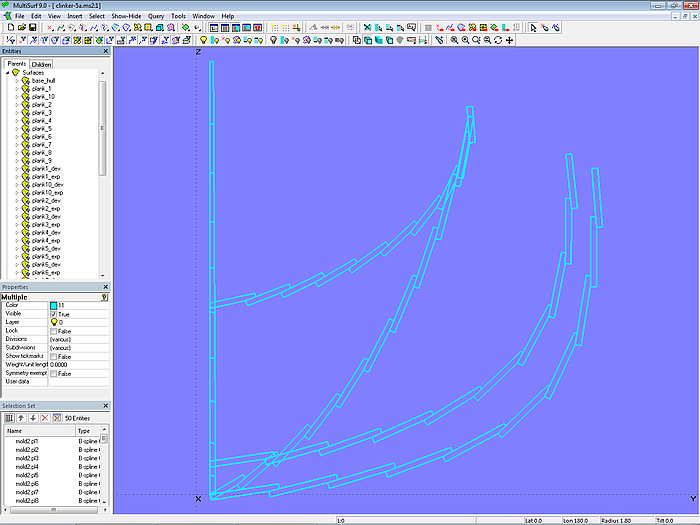
Modell clinker-5a.ms2 – flexible Konstruktion der Planken mit Variablen und Formeln
Alle Planken gleiche Breite
Haben alle Mallpunkte voneinander den gleichen Abstand, ist Planke 1 von aussen gesehen schmaler und Planke 10 breiter als die übrigen gleich breiten Planken 2 – 9. Dies ist in Modell clinker-5b.ms2 gezeigt.
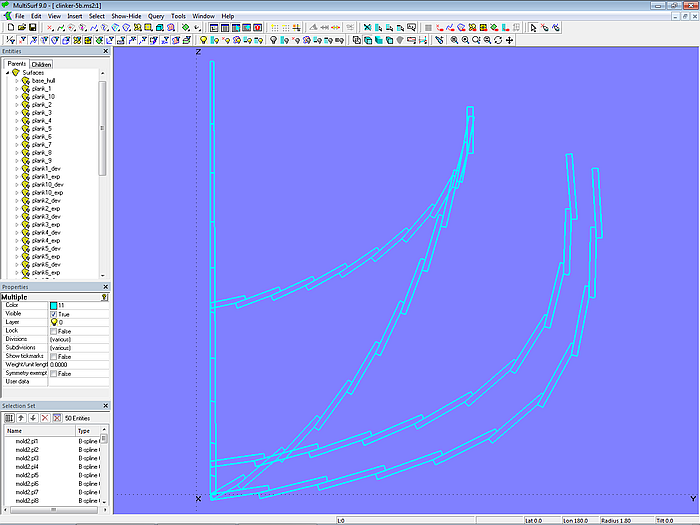
Modell clinker-5b.ms2 – flexible Konstruktion der Planken mit Variablen und Formeln
Verschiedene Breiten
Gleich breite Planken an einem Mall ist kein Muss. Vielleicht soll die die oberste Planke etwas breiter sein, die unterste Planke im geraden Bodenbereich ebenfalls, aber im Kimmbereich wären schmalere Planken zweckmäßig. Auch die Plankenstärken können unterschiedlich sein. Dann brauchen wir nur eine Reihe weiterer Formeln.
Betrachten wir dazu Modell clinker-6.ms2. Die 10 Plankengänge teilen sich auf in 4 Bodengänge, Dicke 0,014 m, in 5 Seitengänge, Dicke 0,013 m und in den Schergang, Dicke 0,017 m. Die Variable thickness_planks_bottom bestimmt die Stärke der Bodenplanken, Variable thickness_planks_side die Stärke der Seitenplanken und Variable thickness_sheerstrake die Stärke des Schergangs. Variable landing_factor ist der Faktor für die Landung, hier gewählt 1,8. Die jeweilige Breite der Landung der Plankengänge berechnen die Formeln landing_planks_bottom, landing_planks_side und landing_sheerstrake.
Gesucht sind nun die Breite der Bodenplanken, der Seitenplanken und des Schergangs.
Mit
bBoden – Breite Bodenplanke
bSeite – Breite Seitenplanke
bSchergang – Breite Schergang
G – Schmiegeumfang
gilt:
4 * bBoden + 5 * bSeite + 1 * bSchergang = G
Mit der Annahme:
bBoden = 1,25 * bSeite
bSchergang = 1,2 * bSeite
folgt dann:
4 * (1,25 * bSeite) + 5 * bSeite + 1,2 * bSeite = 11,2 * bSeite = G
bSeite = G / 11,2
Die Formeln br_pl_side_mold3 ... br_pl_side_mold5 ermitteln die Breite der Seitenplanken (5 – 9) an den Mallen. Die Formeln br_pl_bot_mold3 ... br_pl_bot_mold5 berechnen entsprechend die Breite für die Bodenplanken (1 – 4), sowie br_pl_sheer_mold3 ... br_pl_sheer_mold5 die Breite für den Schergang (Planke 10).
Die Werte dieser Variablen und Formeln werden dann für die Definition der Kontrollpunkte für die Plankennähte und der Plankenquerschnitte verwendet. Bei der beschriebenen Methode werden die Mallpunkte also nicht manuell angeordnet, sie ergeben sich aus den Vorgaben. Die Punkte von Mall 1 und Mall 2 sind frei angeordnet, damit die Plankennähte nicht wie bei Modell clinker-1.ms2 mit deutlichem Wendepunkt verlaufen.
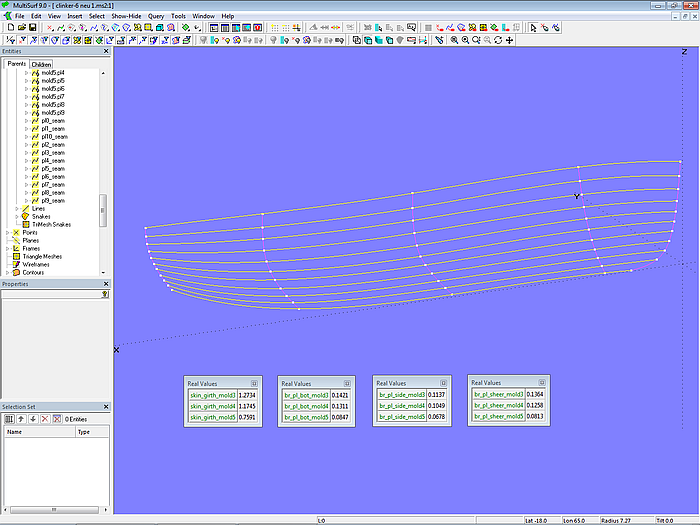
Modell clinker-6.ms2 – Verlauf der Plankennähte und Ergebnisse der Berechnung der Gurtmasse und Plankenbreiten der Mallen
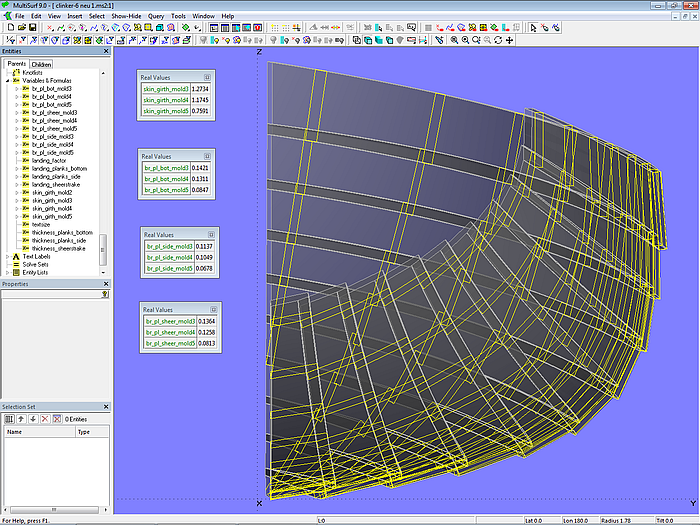
Modell clinker-6.ms2 – Planken und Spantquerschnitte
4 Klinkeraussenhaut-Methode
In Kapitel 2, Abschnitt 2.5 wird beschrieben, wie aus den Plankenquerschnitten an den Mallen auch eine Aussenfläche des Klinkerrumpfes konstruiert werden kann. Besteht die Hauptaufgabe aber darin, für ein GfK-Boot eine lediglich nach Klinkerbauweise aussehende Rumpffläche zu modellieren, kann das in Modell clinker_skin-1.ms2 gezeigte Verfahren angewendet werden („Klinker-Look“). Es erfordert wesentlich weniger Konstruktionsaufwand.
Bei der Klinkeraussenhaut-Methode wird für jedes Mall zuerst eine Intersection Snake erzeugt, dazu im Abstand der Plankendicke eine Offset Curve. Im Gegensatz zur Plankenquerschnitt-Methode mit Mallen auf der Offset Surface base_hull_off sind diese Mallen Intersection Snakes durch base_hull, die Basisfläche des Rumpfes. Mall 1 ist die Vorderkante von base_hull.
Dann werden auf der Mallkurve im gleichen Abstand liegende Arc-length Rings mit einer Serie von Beads auf der Offset Curve zu einer im Zickzack verlaufenden B-spline Curve verbunden. Diese wiederum ist dann Stützkurve für eine C-spline Lofted Surface als klinkerartige Aussenfläche.
Sehen wir uns das für Mc3 an Hand von Mall 3 genauer an.
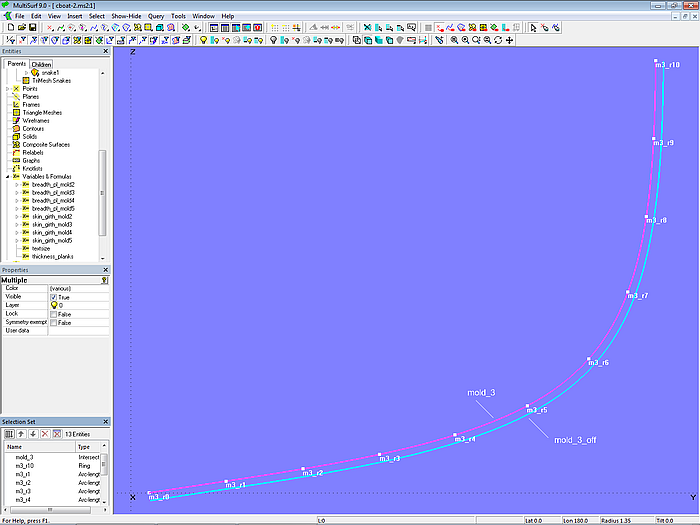
Modell clinker_skin-1.ms2 – Mall 3 für eine klinkerartige Aussenhaut
Auf der Intersection Snake mold_3 liegen die Arc-length Rings m3_r1, m3_r2 ... m3_r8, m3_r9. Ihr Abstand voneinander ist gleich, berechnet mit der Formel breadth_pl_mold3. Von mold_3 ist die Offset Curve mold_3_off abhängig; die Variable thickness_planks bestimmt ihren Abstand. Auf mold_3_off liegen die Beads m3_e0, m3_e1, m3_e2 ... m3_e8, m3_e9.
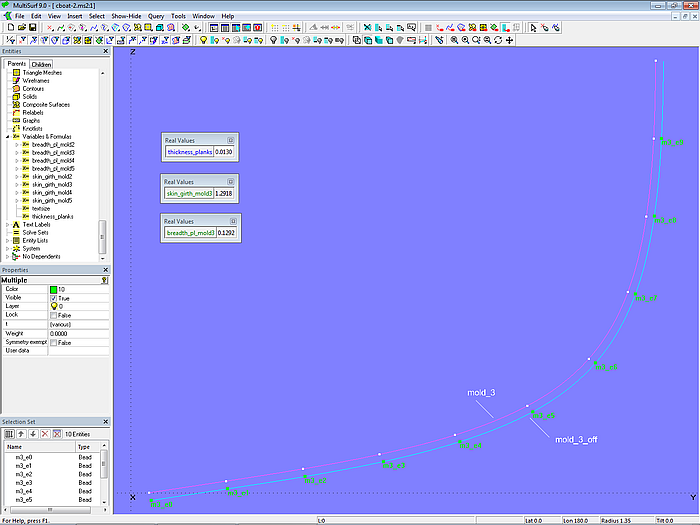
Modell clinker_skin-1.ms2 – Mall 3 für eine klinkerartige Aussenhaut
Mit diesen Beads auf mold_3_off und den Arc-length Rings auf mold_3 als Kontrollpunkte ist die B-spline Curve mc3_clinker_skin (degree = 1) definiert.
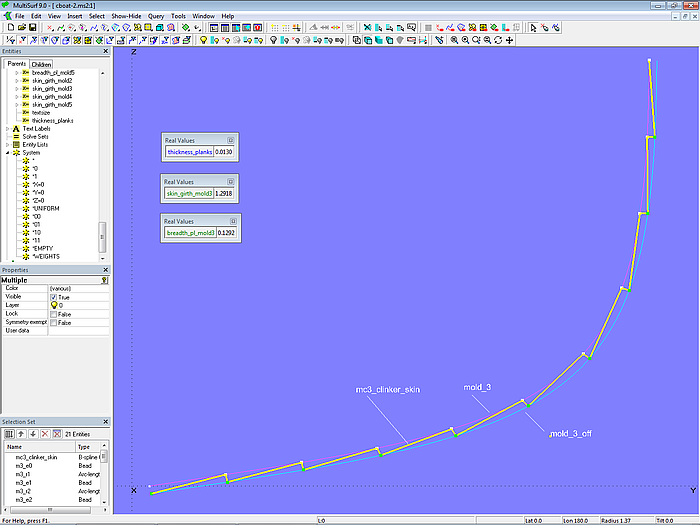
Modell clinker_skin-1.ms2 – Masterkurve an Mall 3 für eine klinkerartige Aussenhautfläche
Verschiebt man die Beads m3_e1, m3_e2 etc. ändert sich auch die Kurve mc3_clinker_skin. Je nach der Position der Beads kann zum Beispiel der zwischen den Punkten m3_r1, m3_e1 und m3_r2 aufgespannte Kantenwinkel größer als 90° sein, oder wie bei den Punkten m3_r3, m3_e3 und m3_r4, kleiner als 90°.
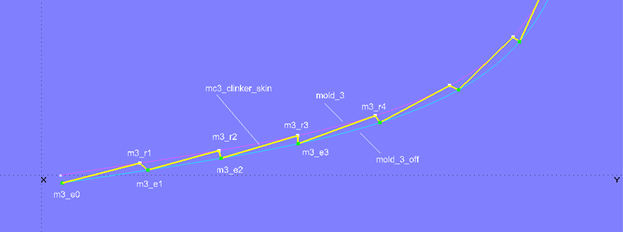
Modell clinker_skin-1.ms2 – Abhängigkeit der Plankenstufen von der Position der Kontroll-Beads auf mold_3_off
Es stellt sich also die Frage: auf welchen Positionen müssen die Beads m3_e1, m3_e2 etc. liegen, wenn zum Beispiel der Kantenwinkel überall 90° betragen soll?
Um diese Frage zu beantworten, werden zum Modell clinker_skin-1.ms2 eine Reihe von Halbkreisen (Arc, Type = 6) hinzugefügt. Point1 (Startpunkt) ist jeweils ein Mallpunkt auf mold_3, Point2 (Mittelpunkt) ist der entsprechende Bead auf mold_3_off, Point3 ist der nachfolgende Mallpunkt. Arc m3_arc1 ist zum Beispiel erzeugt mit m3_r1 für Point1, m3_e1 für Point2 und m3_r2 für Point3.
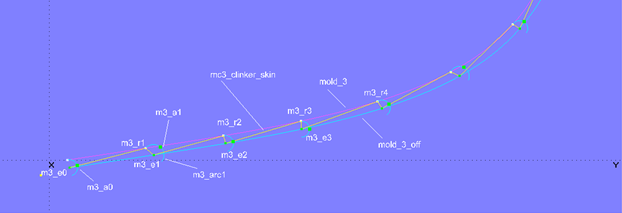
Modell clinker_skin-1.ms2 – Hilfskonstruktion für eine regelmäßige Anordnung der Kontroll-Beads
Auf dem Halbkreis m3_arc0 liegt der Bead m3_a0. Auf den anderen Halbkreisen liegen ebenfalls Beads, es sind allerdings Copy Beads (m3_a1, m3_a2 etc.) mit m3_a0 als Support. Das heißt, wird Bead m3_a0 auf Arc m3_arc0 verschoben, sich also sein Parameterwert t verändert, werden die Copy Beads auf allen anderen Halbkreisen auf den gleichen t-Wert gesetzt.
Was bringt uns das nun? Setzen wir Bead m3_a0 auf t = 0.5 und verschieben dann m3_e1 auf mold_3_off solange, bis die B-spline Curve mc3_clinker_skin durch den Copy Bead m3_a1 verläuft. Genau dann beträgt der Kantenwinkel zwischen den Punkten m3_r1, m3_e1 und m3_r2 90°.
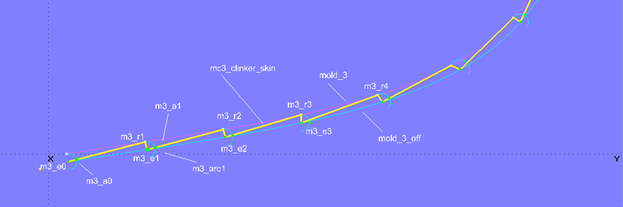
Modell clinker_skin-1.ms2 – Hilfskonstruktion für gleiche Winkel zwischen den Plankenkanten
Denn die t-Position eines Beads auf einem Halbkreis entspricht einem Winkel zwischen Bogenanfang, Mittelpunkt und Punkt auf dem Bogen. Für t = 1 beträgt der Winkel 180°, für t = 0.25, ist der Winkel 45°. Soll der Winkel 95° betragen, muß man den Kurvenpunkt, also unseren „Master“-Bead m3_a0, auf t = 0.5278 (= 0.5 x 95 / 90) setzen.
Somit haben wir Anhaltspunkte zur Positionierung der Beads auf der Offset Curve mold_3_off. Wir müssen m3_e1, m3_e2 etc. so verschieben, dass mc3_clinker_skin überall durch unsere Hilfspunkte verläuft. Dann entspricht der Kantenwinkel dem Produkt aus t x 180°.
Das Verschieben der Beads erfolgt manuell. Mit einem externen Programm kann über MultiSurfs API die Anordnung der Beads auch automatisiert werden.
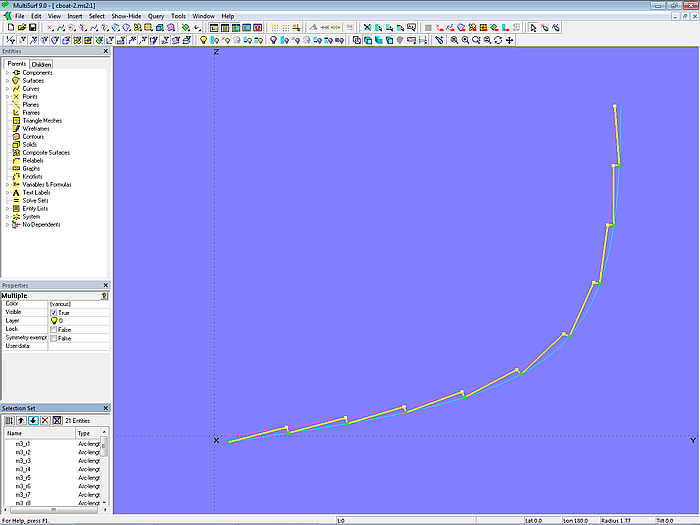
Modell clinker_skin-1.ms2 – Masterkurve mc3_clinker_skin an Mall 3 mit gleichförmigen Plankenstufen
Dies ist Modell clinker_skin-1.ms2. Mit seiner Hilfe ist die Komponente cl_skin.mc2 erstellt. Sie benötigt als Eltern das Mall (Snake) und die Mallpunkte (Rings), als Ergebnis liefert sie die fertige Masterkurve für die Aussenhaut.
In Modell clinker_skin-2.ms2 sind mit dieser Komponente die weiteren Masterkurven mc2_clinker_skin, mc4_clinker_skin und mc5_clinker_skin an den Mallen 2, 4 und 5 eingefügt.
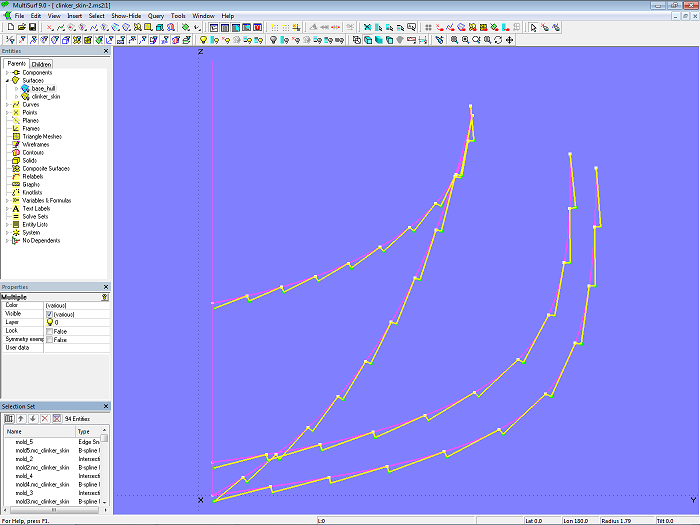
Modell clinker_skin-2.ms2 – mit Component eingefügte Masterkurven an Mall 2 – Mall 5 mit gleichförmigen Plankenstufen
Nun fehlt noch die Mc1 für mold_1 am Vorsteven. Sie darf nicht im Zickzack verlaufen wie die anderen Mcs, da am Vorsteven die Plankenkanten auslaufen sollen. Darum wird Mc1 durch die PolyCurve mc1_clinker_skin gebildet. Diese setzt sich sowohl aus den SubSnakes zwischen den auf mold_1 liegenden Arc-length Rings sowie diesen Arc-length Rings selbst zusammen. Sie hat folglich die gleiche Form wie mold_1. Mit Mc1 bis Mc5 ist schließlich die C-spline Lofted Surface clinker_skin definiert.
Warum wird als Mc1 für clinker_skin nicht direkt die EdgeSnake mold_1 verwendet, sondern aufwendig eine PolyCurve mit gleicher Form konstruiert? Der Grund hierfür ist, dass die Parametrisierung von Mc1 die gleiche sein muß wie die der anderen Mcs. Ansonsten würden die u-Parameterkurven von clinker_skin nicht die Plankenkanten abbilden, sondern an unpassenden Positionen beginnen.
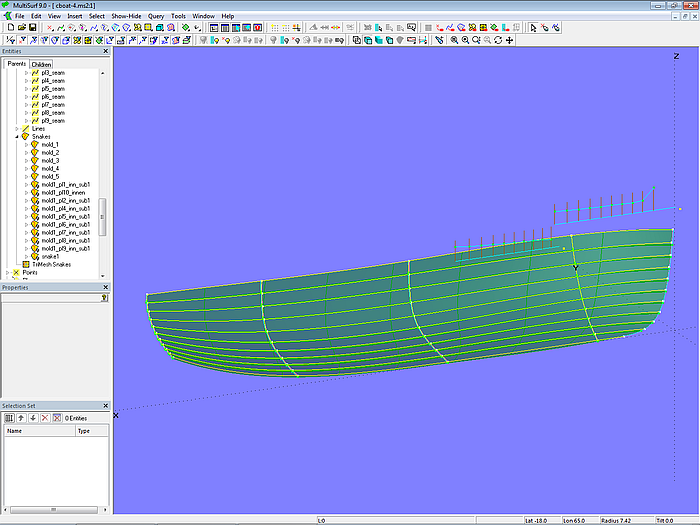
Modell clinker_skin-2.ms2 – klinkerartige C-spline Lofted Surface
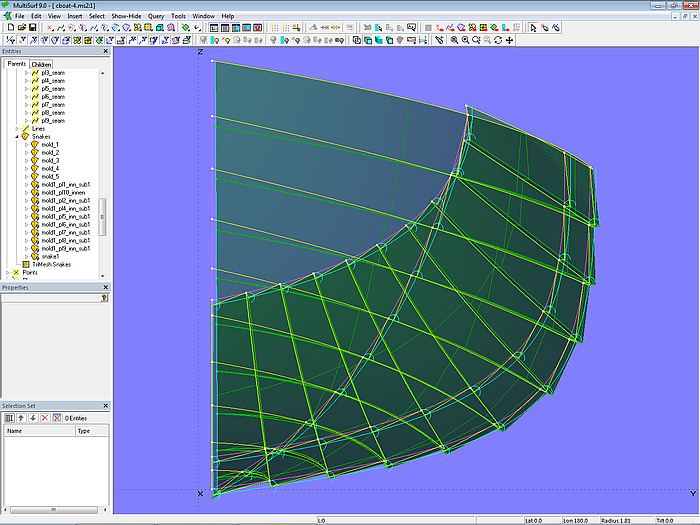
Modell clinker_skin-2.ms2 – klinkerartige C-spline Lofted Surface
5 Beispiele
5.1 Beiboot (Plankenquerschnitt-Methode)
In Modell dinghy.ms2 wird die Konstruktion eines Beiboots in Klinkerbauweise nach der Plankenquerschnitt-Methode gezeigt. Zusätzlich sind Vorsteven und Kiel modelliert.
Die Basisfläche des 2,40 m langen Rumpfes ist die von 5 B-spline Masterkurven gestützte C-spline Lofted Surface base_hull. Mc1 läuft tangential in die Bodenkontur ein. Diese Verbindung ist festverdrahtet durch die Verwendung des Tangent Points p14 als vorletzten Cp für mc1. Mc5 ist eine B-spline Snake auf der Basisfläche des Spiegels.
Sponung
Da außer den Klinkerplanken auch Vorsteven und Kiel konstruiert werden sollen, benötigen wir den Verlauf der Sponung am Bootsrumpf. Die Sponung wird gebildet durch die aneinanderstoßenden Flächen von Sponungsfront und Sponungsseite. Die Außenkante der Sponungsfront bildet am Vorsteven die EdgeSnake stem_rabbet_out entlang der Vorderkante von base_hull. Entlang der Unterkante (Bodenkontur) ist dies die EdgeSnake keel_rabbet_out. Die Innenkante der Sponungsfront bilden die entsprechenden EdgeSnakes stem_rabbet_in und keel_rabbet_in der Offset Surface base_hull_off, der um die Plankenstärke nach innen versetzten Rumpfoberfläche.
So weit, so gut. Bei genauerer Betrachtung dieser Kurven fällt aber der unregelmäßige Verlauf der Innenkante auf, und zwar dort, wo die beiden Sponungskurven stem_rabbet_in und keel_rabbet_in zusammenstoßen. Auch die Offset Surface base_hull_off zeigt diese Unstetigkeit.
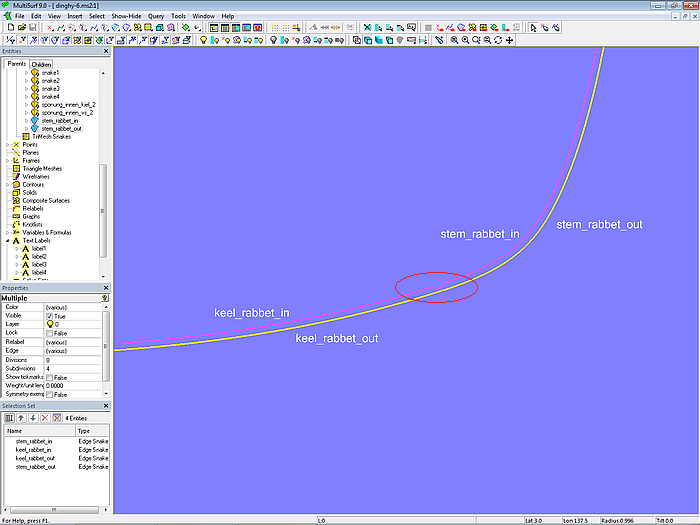
Modell dinghy.ms2 – die Sponungskurven stem_rabbet_in und keel_rabbet_in stoßen unstetig zusammen.
Um eine Offset Surface zu erzeugen, muß in jedem durch seine u- und v-Koordinaten definierten Flächenpunkt der Basisfläche die Tangentialebene und ihre Flächennormale ermittelt werden. Auf dieser wird dann ein Punkt im gewünschten Abstand bestimmt.
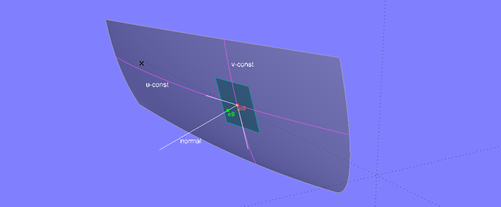
Die Tangenten an die uv-Parameterkurven spannen im Flächenpunkt m0 die Tangentialebene auf. Die Flächennormale steht senkrecht dazu.
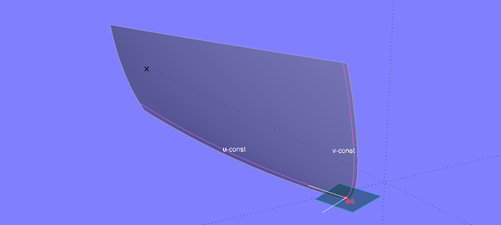
Stoßen zwei Flächenkanten tangential aneinander, wird der Winkel zwischen den Tangenten immer kleiner, je näher m0 dem Verbindungspunkt kommt.
Wenn zwei Kanten einer Fläche tangential aneinander stoßen, ist im Verbindungspunkt der Winkel zwischen den Tangenten an die zu seinen u- und v-Koordinaten zugehörigen Parameterkurven u_const und v_const gleich Null. Die Tangentialebene degeneriert zu einer Linie, eine Flächennormale und damit eine Offset Surface existiert für diesen Punkt nicht.
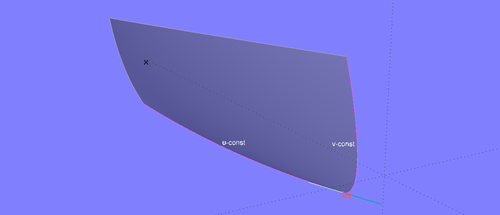
Im Verbindungspunkt der Flächenkanten degeneriert die Tangentialebene zu einer Linie.
MultiSurf-spezifisch ist hier, dass dennoch eine Offset Surface berechnet wird. Allerdings hat sie einen Sprung, da entlang der Kanten an der Verbindungsstelle nur bis zu einem Grenzwert die Flächennormale bestimmt wird. Entsprechend unstetig stoßen ihre EdgeSnakes aneinander.
Während die beiden Sponungs-Snakes von base_hull stetig verlaufen, muß die ungleichförmige Verbindung der Snakes auf der Offset Surface base_hull_off korrigiert werden. Dazu setzen wir auf Snake stem_rabbet_in den Ring ring1 und davon abhängig den Tangent Point pt5. Entsprechend auf Snake keel_rabbet_in den Ring ring2 mit dem Tangent Point pt6. Mit diesen vier Punkten ist die somit tangential mit beiden Sponungskurven verbundene B-spline Curve rabbet_in_fix definiert.

Modell dinghy.ms2 – B-spline Curve keel_rabbet_fix überbrückt die Unstetigkeit zwischen Vorsteven- und Kielsponung innen.
Mit Bead bead6 wird diese Kurve dann geteilt in die SubCurves stem_rabbet_in1 und keel_rabbet_in1. SubSnake stem_rabbet_in2 ist ab ring1 das Kurvenstück auf stem_rabbet_in. Entsprechend definiert SubSnake keel_rabbet_in2 den Kurvenbereich ab ring2 bis zum Ende von keel_rabbet_in entlang des Kiels. Schließlich werden diese Kurventeile zu den PolyCurves stem_rabbet_in_fixed und keel_rabbet_in_fixed verbunden.

Modell dinghy.ms2 – Komponenten der PolyCurves stem_rabbet_in_fixed und keel_rabbet_in_fixed
Durch Verschieben der Cps der B-spline Curve rabbet_in_fix muß dafür gesorgt werden, dass die Innenkante der Sponung von Kiel und Vorsteven harmonisch zur Aussenkante verlaufen.

Modell dinghy.ms2 – Flächen der Sponungsfront am Vorsteven und Kiel
Plankenverlauf
Das Beiboot soll mit 9 Planken mit je 8 mm Dicke über 7 Mallen konstruiert werden. Die Breite der obersten Planke an Mall 4 soll 0,120 m betragen. Die Breite an den übrigen Mallen wird mit Hilfe einer Formel im Verhältnis des jeweiligen Gurtmaßes zum Gurtmaß von Mall 4 berechnet. Die Mallpunkte (Arc-length Rings) für die Breite von Planke 1 werden frei positioniert. Ebenso die Mallpunkte an Mall 2. An den übrigen Mallen werden mit Hilfe von Formeln die Arc-length Rings für die Mallpunkte so angeordnet, dass Planke 2 bis Planke 8 jeweils gleich breit ist.
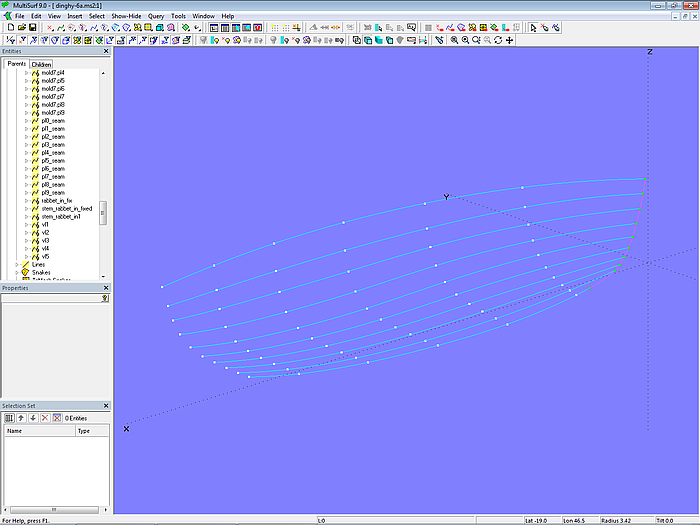
Modell dinghy.ms2 – Verlauf der Plankennähte
Planken
Entsprechend der Konstruktion der Planken für das Arbeitsboot sind auch die Planken für das Modell dinghy.ms2 modelliert. Jede Planke wird gestützt von 7 Querschnitts-Masterkurven.
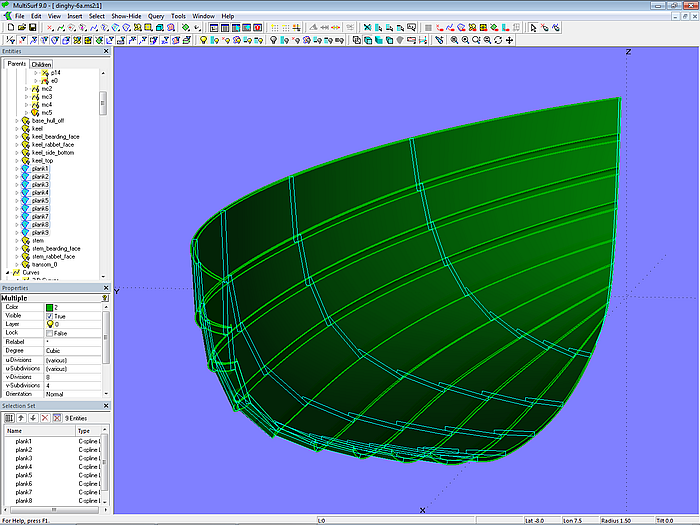
Modell dinghy.ms2 – Planken und Stützkurven
Steven
Vom Steven sind bereits die Kurven der Aussen- und Innenkante der Sponungsfront konstruiert. Dies sind die PolyCurve stem_rabbet_in_fixed und EdgeSnake stem_rabbet_out. Wir brauchen noch die Stevenfront, die Stevenseite aussen, die Sponungsseite, die Stevenseite innen sowie Rückseite des Stevens.
Beginnen wir mit der Aussenseite des Steven. Der Überstand zu Vorkante Beplankung (EdgeSnake stem_rabbet_out) soll oben 20 mm betragen, unten 30 mm. Die halbe Breite soll 10 mm betragen. Entsprechend der Bug-Masterkurve mc1 wird hierfür mit ähnlichem Verlauf die mit 5 Cps kontrollierte B-spline Curve curve1 eingefügt. Diese dann auf die Mittschiffsebene (*Y=0) projeziert als Projected Curve curve2. Zwischen curve1 und curve2 ist die Ruled Surface stem_front aufgespannt, und zwischen curve1 und stem_rabbet_out die Ruled Surface stem_outside.
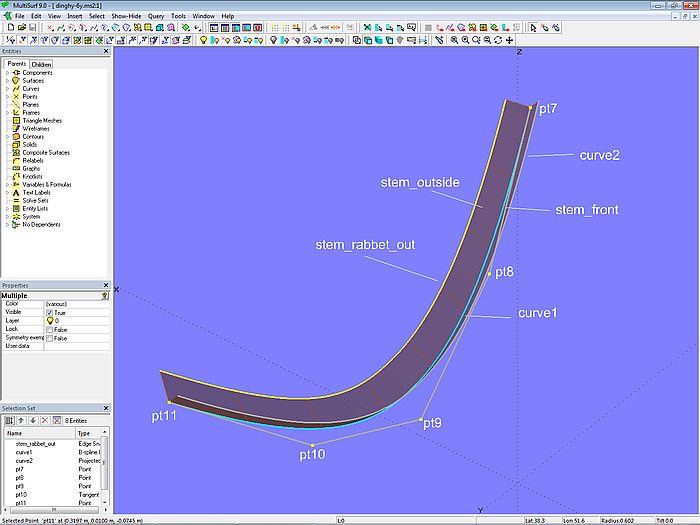
Modell dinghy.ms2 – Konstruktion der Kanten des Vorstevens aussen
Mit ihrer Innenseite liegen die Planken am Vorsteven an der Sponungsseite an. Diese Fläche wird in folgenden Schritten modelliert. Die mit der Sponungsfront gemeinsame Kante der Sponungsseite ist die PolyCurve stem_rabbet_in_fixed. Für die Konstruktion der Außenkante der Sponungsseite liegt auf EdgeSnake stem_rabbet_out der Ring ring3 und der davon abhängige Tangent Point pt12. Beide Punkte bestimmen Line line1. Ebenfalls abhängig von ring3 ist Offset Point pt13. Dieser Punkt wird um line1 um 90° gedreht mit dem Rotated Point pt14. Dieser wiederum wird dann als Projected Magnet m6 auf die Basisfläche base_hull projeziert. In der Procedural Snake snake1 wird diese Konstruktion von m6 für alle Positionen von ring3 wiederholt. Abschließend wird snake1 um die Plankenstärke nach innen versetzt mit Offset Curve stem_bearding.
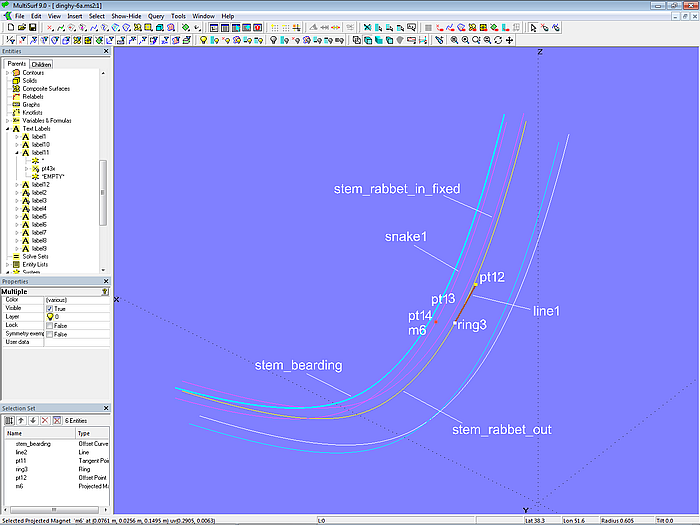
Modell dinghy.ms2 – Konstruktion der Kanten der Sponung
Auf diese Weise entsteht eine Sponungsseite mit konstanter Breite, aufgespannt durch die Ruled Surface stem_bearding_face zwischen der Kurve stem_bearding und der Kurve stem_rabbet_in_fixed./p>
Die Sponungsfront bildet die Ruled Surface stem_rabbet_face zwischen der Kurve stem_rabbet_out und der Kurve stem_rabbet_in_fixed.
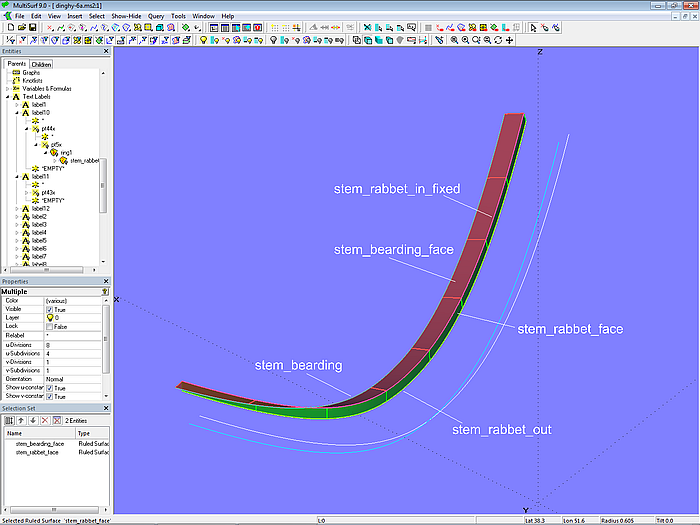
Modell dinghy.ms2 – Front und Seite der Sponung am Vorsteven
Für den Innenteil des Vorstevenbalkens fehlen noch die Kurven, die Höhe und Breite festlegen.Hierfür wird eine prozedurale Konstruktion verwendet, um eine konstante Höhe und Breite der Rückseite zu erhalten. Dazu wird auf der Offset Curve stem_bearding der Bead bead1 gesetzt. Davon abhängig ist der Tangent Point pt16; sein Offset-Wert bestimmt die Höhe des Stevens innen. Von bead1 hängt auch Point pt17 ab; zwischen beiden Punkten verläuft Line line2. Pt16 wird nun um 90°um line2 gedreht durch den Rotated Point pt18. Für alle t-Werte von bead1 wird diese Konstruktion durch die Procedural Curve curve3 wiederholt. Ihre Projektion auf *Y=0 (Mittschiffsebene) ist Projected Curve curve4.
Die Innenseite des Vorstevens bildet nun die Ruled Surface stem_inside zwischen der Kurve stem_bearding und curve3. Die Rückseite des Vorstevens ist die Ruled Surface stem_back zwischen curve3 und curve4.
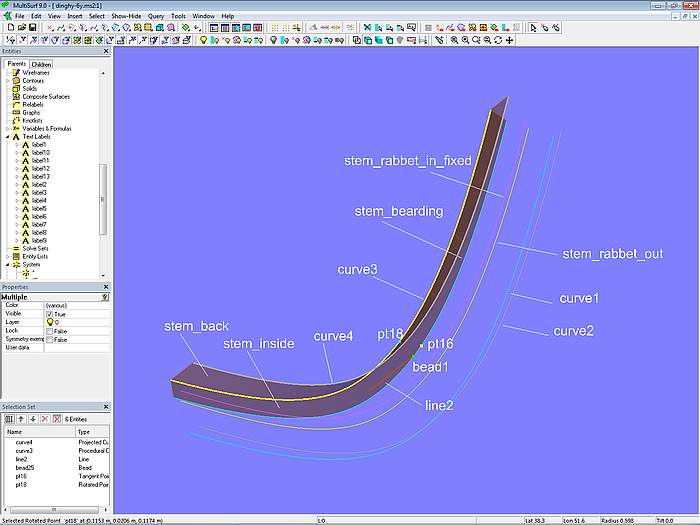
Modell dinghy.ms2 – Innenflächen des Vorstevens
Soviel zu Konstruktion der einzelnen Vorstevenflächen und ihren Kanten.
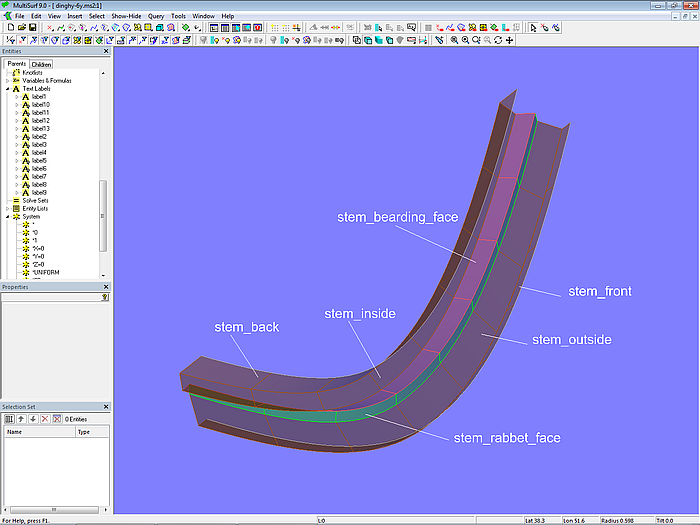
Modell dinghy.ms2 – Flächen am Vorsteven
Kiel
Der Kielbalken besteht aus ebenso vielen Einzelflächen wie der Vorsteven. Die Sponungsflächen haben die gleiche konstante Breite wie am Vorsteven. Höhe und Breite von Innen- und Aussenkiel sind veränderlich.
Die Sponungsfront für den Kiel wurde bereits bei der Korrektur der Innenkante der Sponung konstruiert. Die Konstruktion der Seite der Sponung ist im Prinzip die gleiche wie deren Konstruktion für den Vorsteven. Auf EdgeSnake keel_rabbet_out liegt Ring ring4, davon hängt Tangent Point pt19 ab. Zwischen beiden Punkten liegt Line line3. Bezogen auf ring4 ist Offset Point pt20; der Wert für „Offset“ legt die Breite der Sponungsseite fest. Um line3 wird pt20 um 90° gedreht durch den Rotated Point pt21, der dann auf die Basisfläche des Rumpfes base_hull projeziert wird durch den Projected Magnet m7. Diese Konstruktion einer Flächenkurve mit konstantem Abstand von ihrer Bezugskurve wiederholt die Procedural Snake snake2. Von snake2 hängt wiederum die Offset Curve keel_bearding ab. Die Seite der Sponung ist die Ruled Surface keel_bearding_face zwischen den Kurven keel_rabbet_in_fixed und keel_bearding.
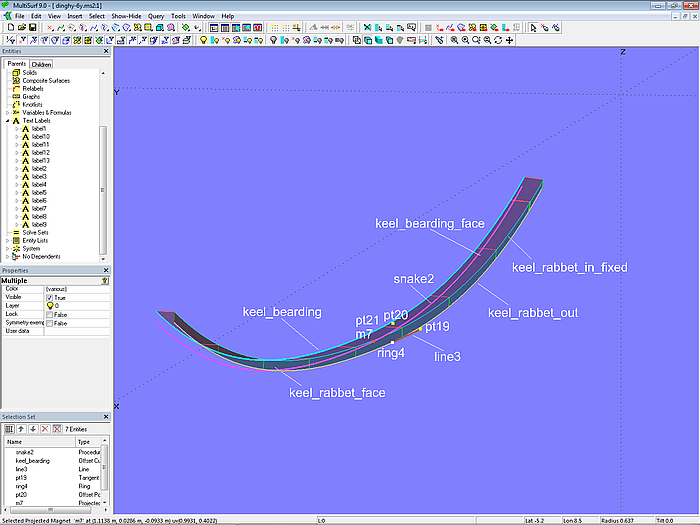
Modell dinghy.ms2 – Konstruktion der Sponungsseite des Kiels
Die Breite und Höhe des Innenkiels wird bestimmt durch die C-spline Curve curve5. Kielseite innen ist die Ruled Surface keel_side_in zwischen keel_bearding und curve5. Die Ruled Surface keel_top verläuft zwischen curve5 und ihrer Projektion curve6 auf die *Y=0-Ebene.
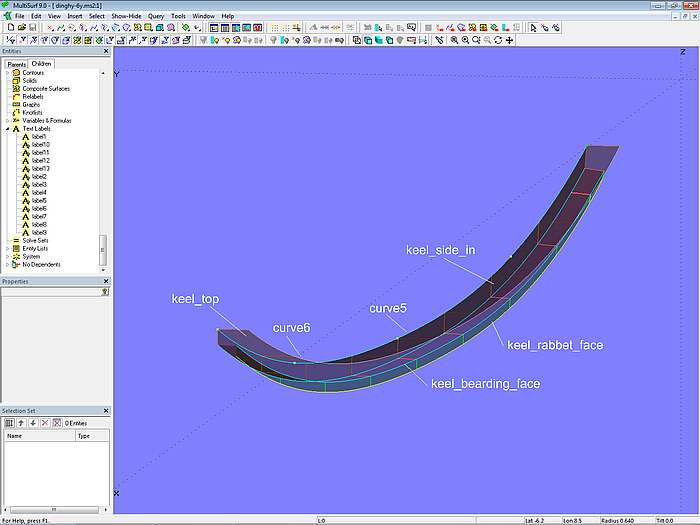
Modell dinghy.ms2 – Konstruktion der Innenseiten des Kiels
Breite und Tiefe des Aussenkiels bestimmt die C-spline Curve curve7. Diese wird auf *Y=0 projeziert als curve8. Seite Innenkiel ist die Ruled Surface keel_side zwischen keel_rabbet_out und curve7. Die Kielsohle bildet die Ruled Surface keel_bottom zwischen curve7 und curve8.
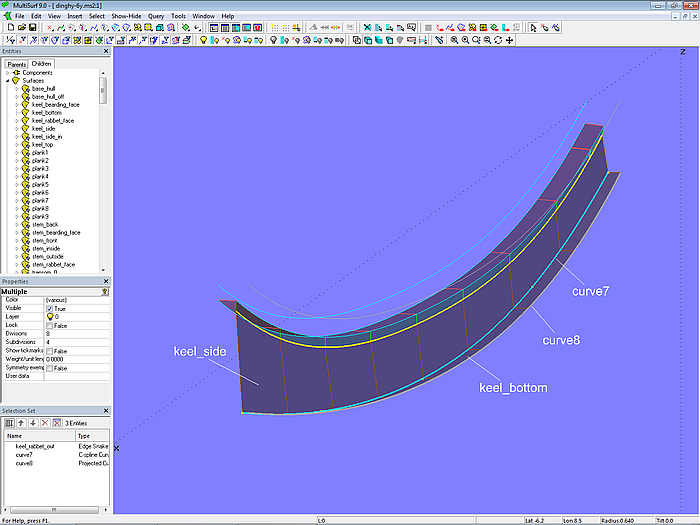
Modell dinghy.ms2 – Konstruktion des Aussenkiels
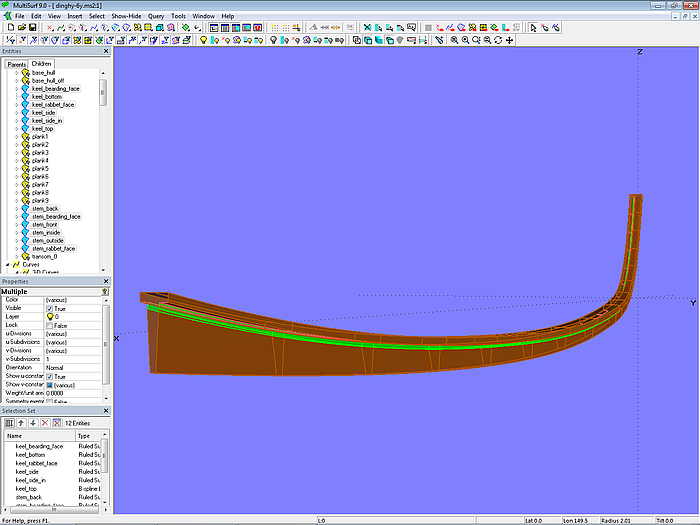
Modell dinghy.ms2 – Konstruktion von Steven und Kiel
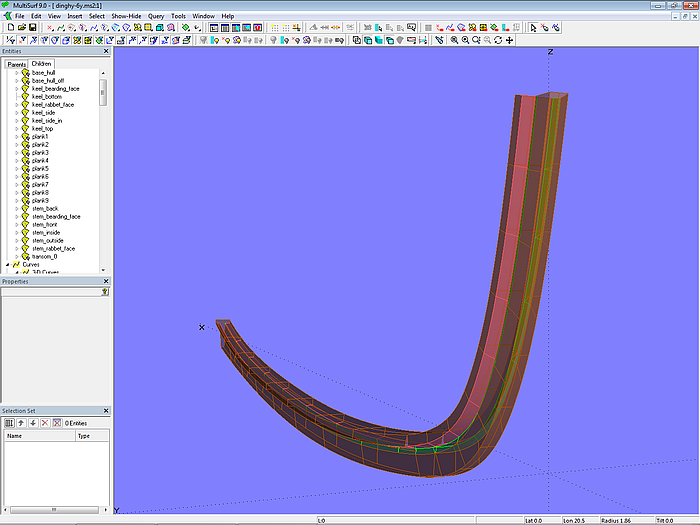
Modell dinghy.ms2 – Konstruktion von Steven und Kiel
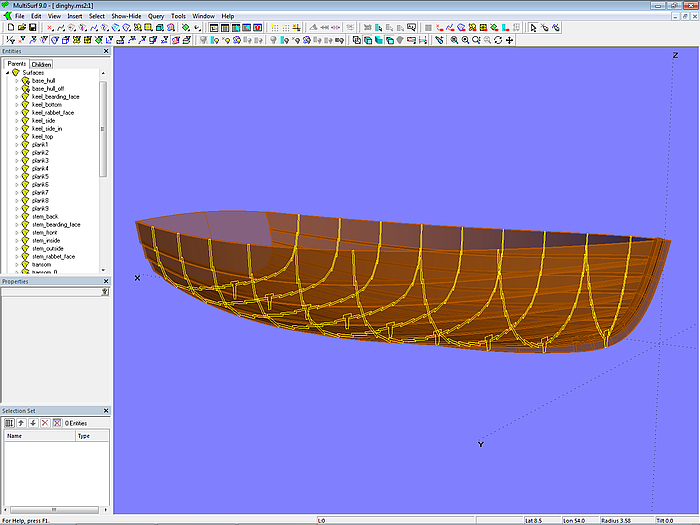
Modell dinghy.ms2 – Klinkerrumpf mit Steven und Kiel
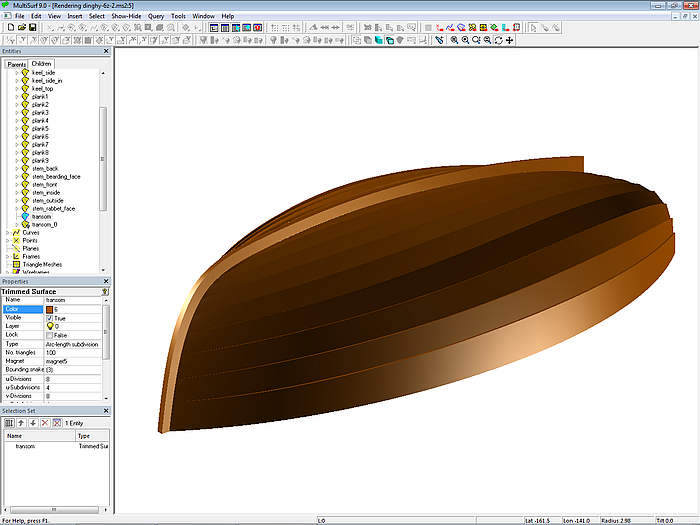
Modell dinghy.ms2 – Klinkerrumpf mit Steven und Kiel
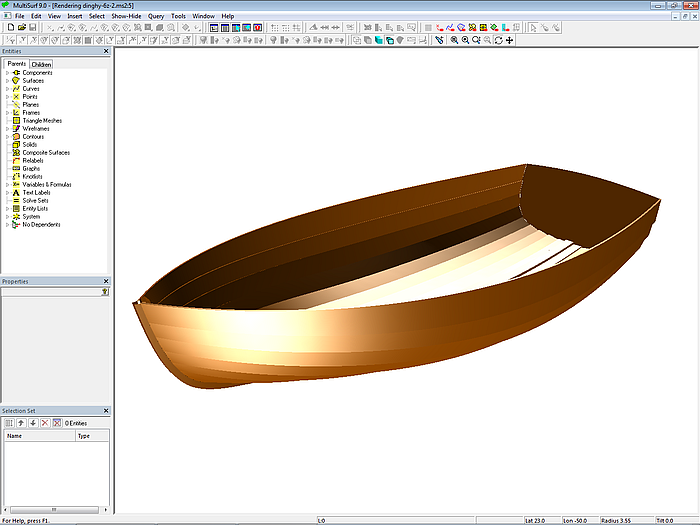
Modell dinghy.ms2 – Klinkerrumpf mit Steven und Kiel
So weit zum Geometriemodell dinghy.ms2 des Beiboots.
5.2 Segelboot (Klinkeraussenhaut-Methode)
Modell centerboarder.ms2 zeigt ein 7 m langes Schwert-Segelboot im „Klinker-Look“. Für den Rumpf wird die Klinkeraussenhaut-Methode angewendet. Basisrumpf ist die C-spline Lofted Surface base_hull, definiert mit 7 B-spline-Mcs mit je 7 Cps. Die nach Klinkerbauweise aussehende C-spline Lofted Surface clinker_skin ahmt einen Rumpf mit 12 Plankengängen nach. Bis auf die oberste Planke haben alle Planken am jeweiligen Mall die gleiche Breite.
Die C-spline Lofted Surface clinker_skin wird von 7 Mallkurven gestützt. Hierfür kommt die Komponente cl_skin_12planks.mc2 zur Anwendung. Dazu vorab die Mallpunkte des Malls auswählen, dann über File/ Component/ Load die Komponente wählen, den Dialog Resolving Parents mit OK bestätigen und die Plankenquerschnitte für das Mall werden generiert.
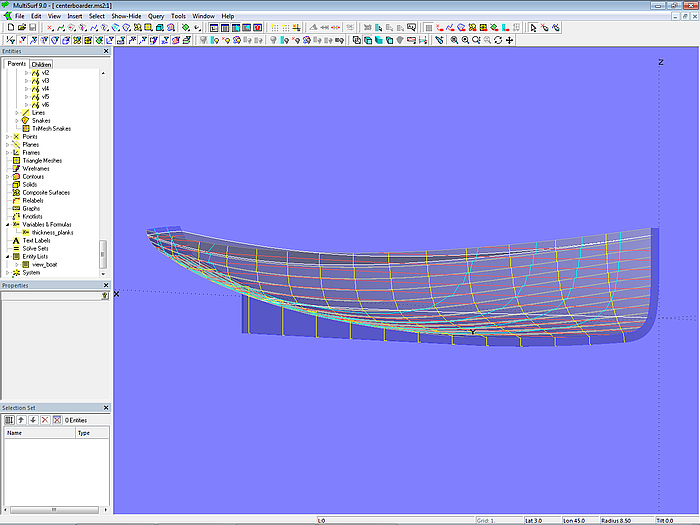
Modell centerboarder.ms2 – Segelbootrumpf im „Klinker-Look“
Man beachte, dass die Planken am Heck ohne Überlappung verlaufen.
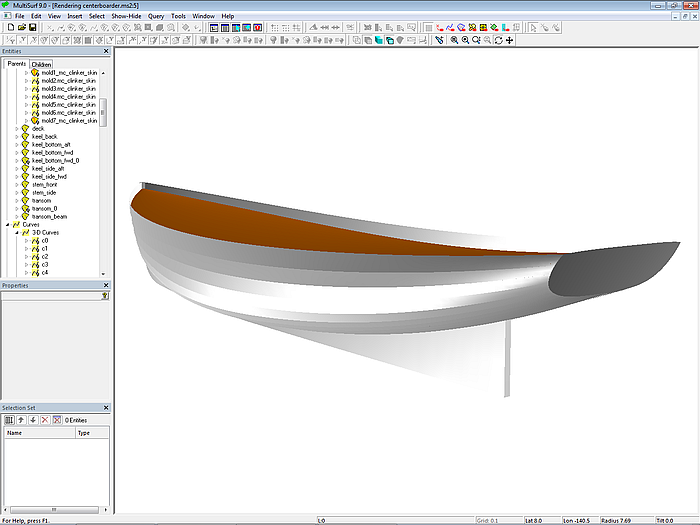
Modell centerboarder.ms2 – Segelbootrumpf im „Klinker-Look“
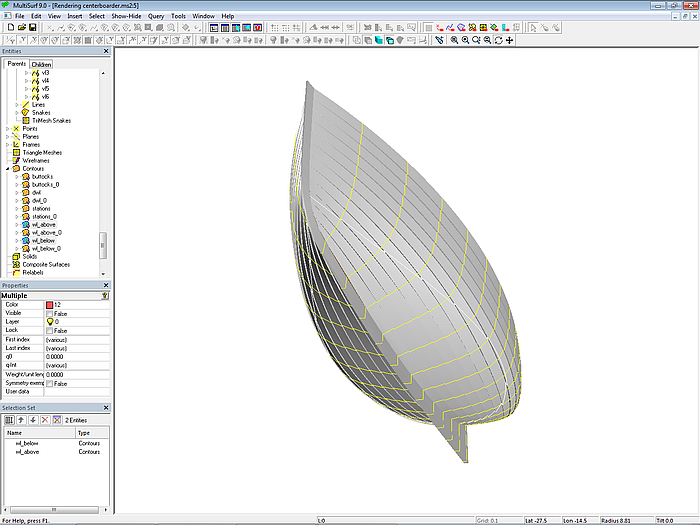
Modell centerboarder.ms2 – Segelbootrumpf im „Klinker-Look“
Anhang 1 – Flächenmodell nach Sentaufmassen
Vorlage: Sentaufmasse
Das Modell diagonal_plan.ms2 zeigt das den Aufmassen zugrundeliegende Sentengerüst. Mit Hilfe von Arc-length Beads werden entlang der Sentlinien die Spantpunkte positioniert. Korrespondierende Spantpunkte sind durch C-spline Curves sowohl in Längs- wie auch in Querrichtung verbunden. Das Modell wird in X-Richtung skaliert, so dass seine Länge 5 m beträgt.
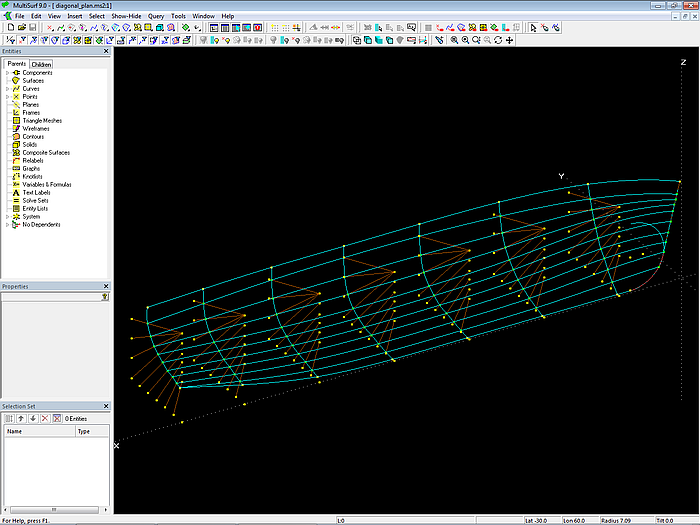
Modell diagonal_plan.ms2 – C-spline Curves verbinden die Spantpunkte im Sentengerüst in Längs- und Querrichtung.
3DA-Wireframe-Datei
Aus dem Modell diagonal_plan.ms2 werden dann die Kurven von Vorsteven, Spanten und Spiegel in der 3DA-Wireframe-Datei pattern.3da abgespeichert (File/ Export 3D/ 3DA wireframe).
Wir haben nun die Angaben in der Aufmasstabelle für den Verlauf der Spanten, des Vorstevens und des Spiegels in eine numerische Form überführt.
Surface Fitting
Die 3DA-Datei pattern.3da ist die Vorlage für die eigentliche rundspantige Rumpffläche. Dazu wird ein neues Modell erstellt, unter dem Dateinamen clinker-0.ms2 gespeichert und über Insert/ Wireframe die 3DA-Datei pattern.3da eingefügt.
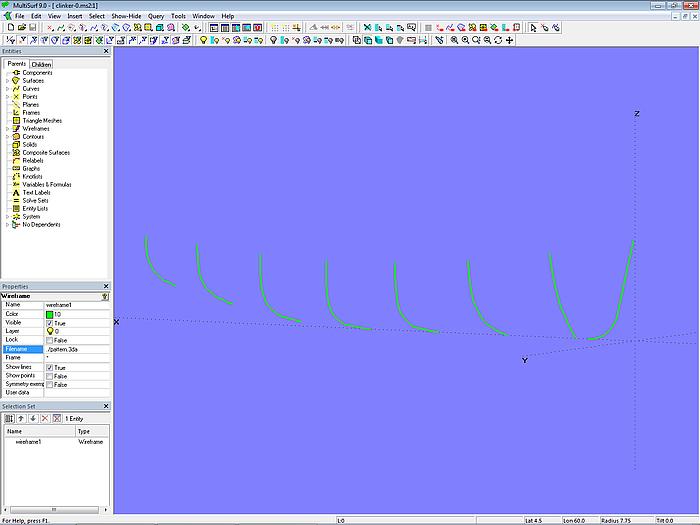
Modell clinker-0.ms2 – die als Vorlage importierte Wireframe-Datei pattern.3a wurde im Modell diagonal_plan.ms2 abgespeichert.
Nun werden für die Wireframe-Kurven B-spline Curves (Degree = 3) mit je 5 Cps erzeugt. Hierfür läßt sich sehr praktisch über Tools/ Special die Funktion B-spline Curve Fit verwenden – in einem Zug werden Kontrollpunkte und Kurven generiert.
Als Masterkurven für die Rundspantform des Arbeitsbootes werden Vorsteven und 4 Spanten ausgewählt. Als Hilfskurven für das Straken verlaufen die C-spline Curves vl_1 bis vl_5 durch korrespondierende Cps.
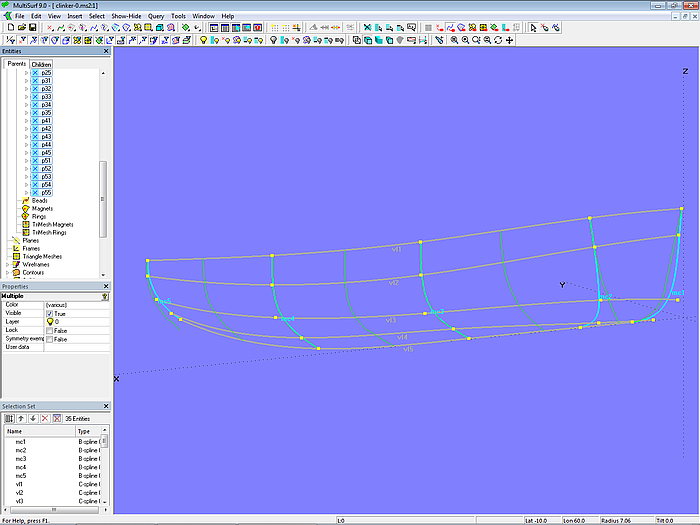
Modell clinker-0.ms2 – Masterkurven (B-spline Curves), Kontrollpunkte und Strakhilfskurven (C-spline Curves)
Vorsteven-Mc (mc1) und Heck-Mc (mc6) weichen etwas von der Vorlage ab. Die Kielfläche achtern kann dadurch etwas größer werden, die Vorstevenkrümmung verläuft gleichmäßiger. Die beiden letzten Cps von mc2 sind etwas nach achtern und außen verschoben, damit sie nicht zu dicht an den Cps von mc1 liegen. C-spline Curves können leicht schwingen, wenn ihre Cps nahe beieinander liegen.
Über die Mcs wird nun die C-spline Lofted Surface base_hull gelegt. Diese wiederum wird von Contours geschnitten, um Spanten, Wasserlinien und Schnitte anzuzeigen. Durch Verschieben der Kontrollpunkte der Mcs wird dann die Rumpfform gestrakt.
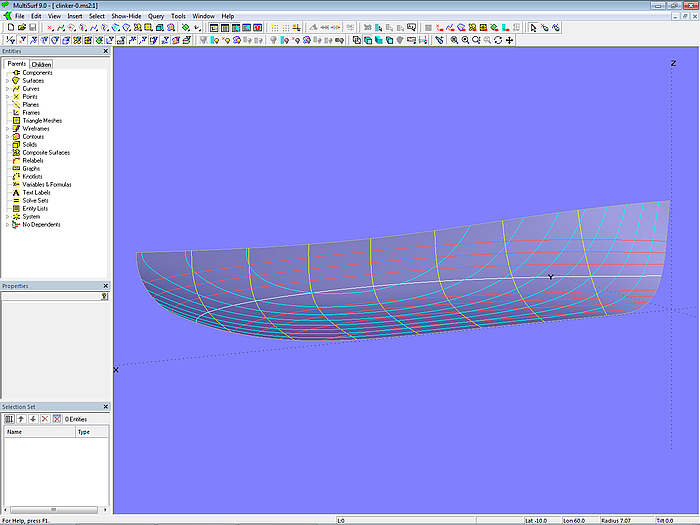
Modell clinker-0.ms2 – Basisfläche des Arbeitsboots
So viel zur Basisfläche für das Arbeitsboot. Von Klinkerplanken ist im Modell clinker_0.ms2 aber weit und breit noch nichts zu sehen. Darum von hier zurück zu Kapitel 2, Abschnitt 2.1, Basisrumpf.
Anhang 2 – graphische Darstellung der Plankenbreiten
In Modell diagram_10planks.ms2 wird gezeigt, wie sich ein Diagramm erstellen läßt, das die Änderung der Breite von 10 Planken über der Malllänge darstellt. Ausgangspunkt als Mall ist die Intersection Snake m2, auf der die Mallpunkte m2_r0, m2_r1 ... m2_r9, m2_r10 liegen. Das gekrümmte Mall wird nun mit Hilfe des Kurventyps Expanded Curve zu der geraden Kurve exp verebnet. Über die Copy Beads e1, e2 ... e9, e10 wird die t-Position der Mallpunkte auf m2 auf die Expanded Curve exp übertragen. Anschließend werden in diesen Kurvenpunkten die senkrechten Lines l1, l2 ... l9, l10 errichtet.
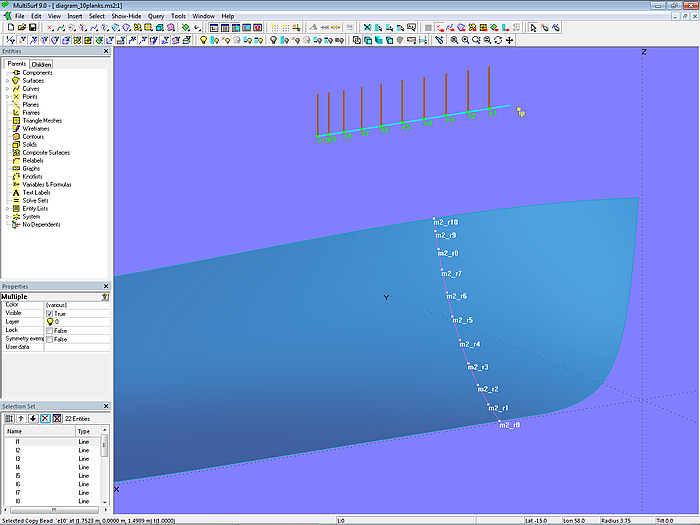
Modell diagram_10planks.ms2 – Diagramm für die Plankenbreite
Nun muß die Plankenbreite an der jeweiligen Line abgetragen werden. Nehmen wir als Beispiel die Breite der Planke 1, also die Distanz zwischen den Punkten m2_r0 und m2_r1. Im Schritt 1 wird diese mit Hilfe des Copy Points p1_0 zum Fußpunkt e1 von Line l1 kopiert. Dann wird im Schritt 2 Line l1 geschnitten im Intersection Bead d_pl1. Hierbei werden als Eltern e1 für Mirror/surface und p1_0 für Point eingesetzt. Was bedeutet das? Da Mirror/surface ein Punkt ist, ist das schneidende Objekt für l1 eine Kugel mit Mittelpunkt e1 und einem Radius gleich der Entfernung e1 – p1_0.
Analog werden die anderen Plankenbreiten im Diagramm eingetragen. Abschließend werden dann die Intersections Beads d_pl1, d_pl2 ... d_pl9, d_pl10 duch eine B-spline Curve mit Degree = 1 verbunden.
Somit entsteht ein Schaubild, dass den Verlauf der Plankenbreite über der Malllänge zeigt.
Wird die Position der Mallpunkte verändert, ändert sich der Graph entsprechend. Auf diese Weise hat man ein Hilfsmittel, um die Anordnung der Planken harmonisch zu gestalten.
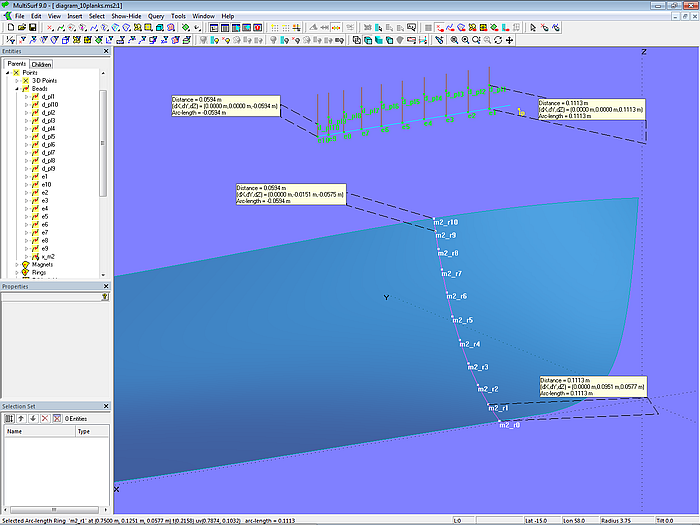
Modell diagram_10planks.ms2 – Diagramm für die Plankenbreite
Component
Um das Diagramm zum Beispiel im Modell clinker-1_final.ms2 einzusetzen, wird mit Hilfe der beiden Entity Lists parents und products und dem Command „selectforcomponent“ über File/ Component/ Save die Komponente diagram_10planks.mc2 erstellt.
======================================================================================